Определение весового коэффициента для регуляризации при измерении желобов колец шарикоподшипников

 

Суслин Владимир Павлович,

кандидат технических наук, доцент, профессор кафедры «Автомобили»,

Джунковский Андрей Владимирович,

кандидат технических наук, доцент кафедры «Стандартизация метрология и сертификация»,

Холодов Дмитрий Алексеевич,

аспирант кафедры «Автоматика и процессы управления».

Московский государственный машиностроительный университете (МАМИ).

 

Definition of weight for the regularization of the measurement gutter ball rings

 

Suslin Vladimir Pavlovich,

candidate Sc. of Engineering professor of the sub-department of «Automobiles»,

Djunkovskiy Andey Vladimirovich,

candidate Sc. of Engineering lecturer of the sub-department of «Standardization, Metrology and Certification»,

Kholodov Dmitry Alexeevich,

graduate of the sub-department of «Automation and Control».

MGMU «MAMI».

 

В статье описан метод определения весовых коэффициентов регуляризирующего звена для плохо обусловленных задач, связанных с измерением деталей, в конструкцию которых входит тороидальная поверхность с малым сектором образующей.

Ключевые слова: координатно-измерительная машина, шариковые подшипники, тороидальные поверхности, плохо обусловленные задачи, регуляризация, l-кривые.

 

This paper describes a method for determining the weights regularizing care for ill-conditioned problems associated with the measurement of parts in a design that includes a toroidal surface with low education sector.

Keywords: cmm, ball-bearings, torus, ill-posed problem, regularization, l-curve.

 

Для полного досборочного контроля шарикоподшипников требуется измерять параметры дорожки качения колец подшипника. Желоб дорожки качения представляет собой тор с сектором образующей окружности около 80º [3]. Результаты процесса измерения такой тороидальной поверхности дорожки качения шарикоподшипника на координатно-измерительных машинах (КИМ) и других технических устройствах, где основу метода определения параметров поверхности представляет метод наименьших квадратов (МНК), сильно зависят от малых изменений входных данных, что недопустимо и приводит к большим погрешностям [2]. Подобные задачи относятся к классу некорректно поставленных или плохо обусловленных задач [1].

В лаборатории САПР Университета машиностроения была исследована возможность и обоснованность применения регуляризации при измерении малых секторов геометрических объектов [4].

На КИМ параметры беговой дорожки шарикоподшипника измеряется минимум по 3м сечениям, в каждом из которых берется 3 точки. Оптимальным количеством точек для измерения является 16, т.е. 4 сечения по 4 точки в каждом [5]. Геометрические параметры тора (центр, ось, радиус и радиус сечения) определялись (МНК). При этом производилась минимизация функции:

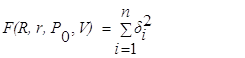                                                                    (1)

где – функция минимизации, содержащая сумму квадратов отклонений измеренных точек от поверхности тора; - искомые параметры тора: радиус кольца, радиус дорожки, центральная точка и вектор оси тора (рисунок 1).

Значение начального приближения для радиуса сечения тора определялось как средний радиус измеренных сечений. Начальные приближения для остальных параметров тора были получены с помощью окружности, проходящей через центры измеренных сечений.

 

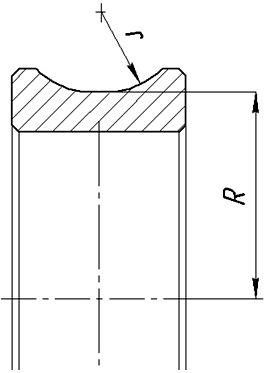
Рис. 1. Внутреннее кольцо подшипника.

 

Эксперименты показали, что решения, полученные описанным способом, не устойчивы к малым изменениям входных данных и задача является плохо обусловленной [2].

В программе ГеоАРМ реализована регуляризация для тороидальных поверхностей путем модификации минимизируемой функции за счет включения в нее отклонений определяемых параметров от их номинальных значений. При этом функция получает вид:

                                                                          (2)

где: reg() – регуляризирующий член, содержащий в себе номинальные значения определяемых параметров и весовой коэффициент.

В чертеже подшипника содержатся такие априорные данные, как радиус желоба беговой дорожки и диаметр беговой дорожки кольца шарикоподшипника. Оба этих параметра должны быть включены в функцию т.к. они взаимосвязаны и за счет изменения одного параметра во время итерационного процесса поиска минимума может быть достигнуто требуемое значение другого, без увеличения суммы квадратов отклонений.

                                                                          (3)

где:  - номинальные значения параметров;  - веса параметров (коэффициенты регуляризации).

Слишком большие весовые коэффициенты сводят задачу к сравнению измеренного тора с его математической моделью т.к. значения параметров тора жестко заданы большими коэффициентами, и сумма квадратов отклонений измеренных точек никак не влияет на решение задачи.

Если веса будут слишком маленькие, то регуляризирующий член не сможет оказать влияние на процесс минимизации и задача по-прежнему останется плохо обусловленной.

Таким образов встает задача выбора весового коэффициента для найденного регуляризирующего параметра. Эффективным и наиболее наглядным методом является метод l-кривой [6-8].

Для проведения эксперимента были сделаны точные математические модели беговых дорожек внутренних и наружных колец подшипников 206А и 307А. Допуск на размеры радиуса желоба беговой дорожки составляет +0.08мм, допуск на диаметр беговой дорожки составляет ±0,025мм.

 

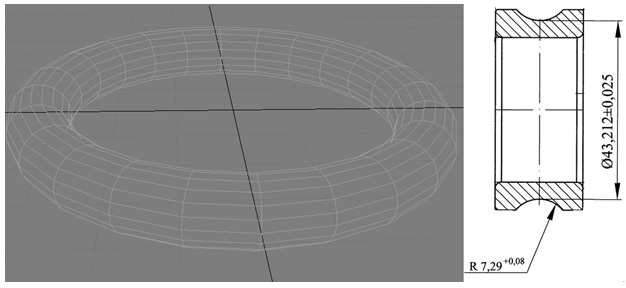
Рис. 2. Модель беговой дорожки кольца шарикоподшипника и допустимые отклонения на размеры.

 

На поверхностях построенных моделях были насчитаны точки, и их координаты испорчены случайными величинами, имитирующими процесс измерения и погрешности, возникающие из-за несовершенства измерительной техники и качества измеряемой поверхности.           

Т.к. при слишком маленьких весовых коэффициентах w регуляризация не приносит результатов, а при слишком больших процесс построения поверхности становится процессом сравнивания ее с точной моделью, необходимо определить оптимальный весовой коэффициент. Для этого был проведен ряд вычислений параметров поверхности с разными весовыми коэффициентами и построен график, по вертикальной оси которого отложена разница между вычисленным измеряемым параметром поверхности и ее оптимальным значением в мм, а по горизонтальной оси отложены значения весовых коэффициентов для регуляризирующего члена. Примеры графиков, полученных в ходе вычислительного эксперимента (когда измерялась математическая модель тора с добавленными случайными погрешностями в точках измерения) изображены на рисунке 3.

 

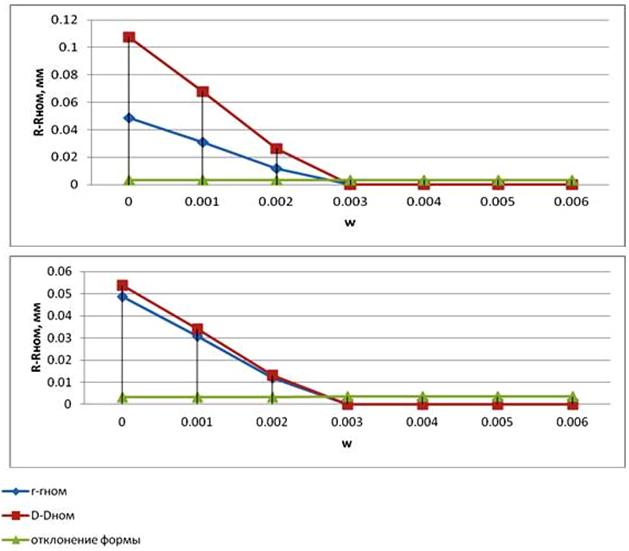
Рис. 3. L-кривые для определения оптимального весового коэффициента регуляризации.

 

Построенные графики наглядно демонстрируют оптимальное значение весового коэффициента в точке перегиба, где w = 0.003. Так же видно, что значение полученных параметров поверхностей при отсутствии регуляризирующего члена (w = 0) отличается от номинального более чем на треть поля допуска, а значит, подобный метод расчета не пригоден для данной плохо обусловленной задачи [9]. О плохой обусловленности задачи свидетельствует то, что изменение отклонения формы на порядок меньше изменения параметров измеряемой поверхности.

Проведение измерительных экспериментов, в ходе которых происходило определение параметров беговых дорожек колец подшипников на КИМ DKM 1-300DP с погрешностью измерений ±(3+L/200) мкм, подтверждает результаты, полученные в ходе вычислительного эксперимента (рисунок 4).

Примеры графиков, полученных при измерение колец шариковых подшипников 307А.01, 206А.01, 8103.01, 8205.01 показаны на рисунке 4.

 

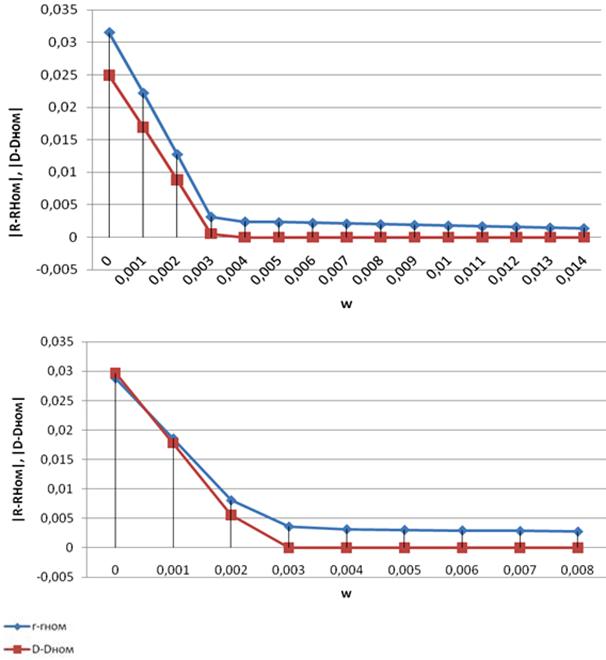
Рис. 4. L-кривые для определения оптимального весового коэффициента регуляризации для колец подшипника 307А.01.

 

Графики построены по данным, полученным после обмеров наружного и внутреннего колец подшипника 307А.01. Они демонстрируют, что при добавлении регуляризирующего звена с малым коэффициентом (до w = 0.002÷0.003) происходит быстрое приближение параметра к номинальным значениям. Погрешность, возникающая при определении параметров построенной поверхности, без регуляризирующего звена составляет 30 мкм, что больше, чем треть поля допуска для данных размеров. Из этого можно сделать вывод о непригодности МНК для построения поверхностей, обмеренных на малой области, без включения в формулу минимизации регуляризирующего члена. Оптимальный весовой коэффициент w находится в точке перегиба графика отклонений полученного значения параметра от его номинальной величины.

 

Литература

 

1.                  А. Н. Тихонов, В.Я Арсенин «Методы решения некорректных задач» - Москва «Наука» 1979.

2.                  Суслин В.П., Джунковский А.В., Холодов Д.А. Плохо обусловленные задачи в геометрических измерениях торовых поверхностей / Известия МГТУ «МАМИ». -2010г. - №1. 7с.

3.                  Суслин В.П., Джунковский А.В., Макаров А.И., Холодов Д.А. Новый метод контроля геометрических параметров колец шарикоподшипников / Автомобильная промышленность. - 2010г. - №11. 6с.

4.                  Суслин В.П., Джунковский А.В., Шутер М.Г. Новый метод определения геометрических параметров объектов при измерениях на малых областях/ Законодательная и прикладная метрология.- 2008.- №6.

5.                  Суслин В.П., Джунковский А.В, Холодов Д.А. Определение оптимального количества точек при измерении колец подшипников качения на координатно-измерительных машинах / Труды 77 международной научно-технической конференции ААИ МГТУ «МАМИ».

6.                  P. C. Hansen The L-curve and its use in the numerical treatment of inverse problems / Department of Mathematical Modelling, Technical University of Denmark, DK-2800 Lyngby, Denmark

7.                  М.Н. Левин, А.В. Татаринцев, А.Э. Ахкубеков. Метод Laplace-DLTS с выбором параметра регуляризации по L-кривой / Физика и техника полупроводников, 2009, том 43, вып. 5

8.                  Д.В. Кирьянов, Е.Н. Кирьянова Вычислительная физика / Полибук Мультимедиа 2006г

9.                  ПМГ 92-2009. Правила по межгосударственной стандартизации. Метрологическая экспертиза проектов межгосударственных и национальных стандартов.

 

Поступила в редакцию 14.11.2013 г.