Использование конформных преобразований для определения эквивалентной диэлектрической проницаемости кабелей связи с парной скруткой

 

Смородинов Дмитрий Александрович,

аспирант Самарского государственного технического университета.

 

Первичные и вторичные параметры передачи и параметры взаимных влияний кабелей связи определяются геометрическими и электрическими параметрами направляющей среды. Не имеющими общего решения являются задачи оценивания рабочей ёмкости кабеля и эквивалентной диэлектрической проницаемости среды между двумя проводниками. Решение данной задачи является актуальным при алгоритмизации автоматического управления параметрами экструдируемой пористой изоляции с введением межконтурной связи, обеспечивающей компенсацию влияния динамической ошибки регулирования одного из параметров (диаметра или диэлектрической проницаемости изоляции) на обобщенный параметр качества кабеля (рабочую ёмкость или волновое сопротивление) путем формирования возмущенного процесса в контуре автоматической стабилизации второго параметра (диэлектрической проницаемости или диаметра изоляции) [1].

Рассматривается задача определения электрических параметров витой пары, которая составляет основу радиочастотных кабелей для передачи данных (LAN-кабель). На рис. 1 показано сечение неэкранированной витой пары, содержащей две жилы, диаметры изоляций которых различны.

 

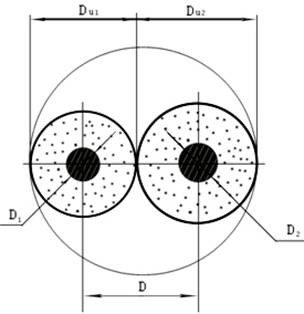
Рис. 1. Сечение LAN-кабеля.

 

Традиционно эквивалентная диэлектрическая проницаемость направляющей среды оценивается как средневзвешенное значение изоляции обеих жил, с учетом соотношения площадей их сечения. Данная оценка характеризуется невысокой точностью, что недопустимо при проектировании и изготовлении кабелей с высокой пропускной способностью.

Чтобы определить эквивалентную диэлектрическую проницаемость ε_экв снова воспользуемся конформным отображением, но теперь отобразим плоскость z (рис. 2) на плоскость t (рис. 3),

 

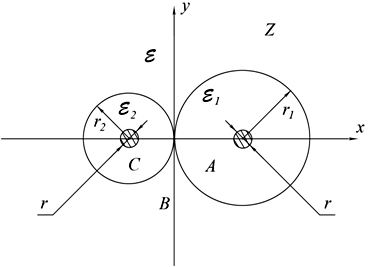
Рис. 2. Взаимоположение жил LAN-кабеля с изоляцией в плоскости Z.

 

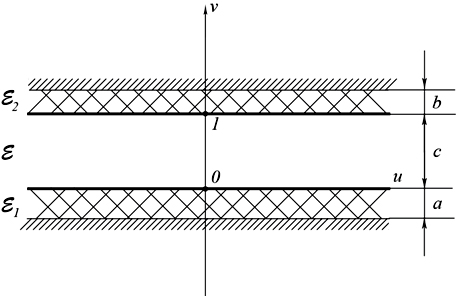
Рис. 3. Результат отображения плоскости z на плоскость t.

 

где

,                                                                                        (1)

а

.                                                                                                                  (2)

Для данного отображения необходимо чтобы выполнялось следующее условие [2]:

.                                                                                                     (3)

Определим u и v, учитывая выражения (1), (2) и (3):

.                                   (4)

Отобразив плоскость z на плоскость t, мы получили плоский конденсатор с бесконечными пластинами. В данном случае представляется возможным определение его диэлектрической проницаемости. Она и будет являться неизвестной эквивалентной диэлектрической проницаемостью среды между двумя проводниками.

Для решения данной задачи полученный конденсатор можно разделить на три последовательносоеденненых конденсатора с однородными диэлектриками между их пластин с соответствующими диэлектрическими проницаемостями: ε₁, ε₂, ε (рис. 4).

 

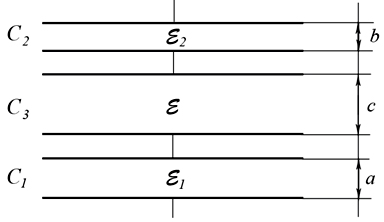
Рис. 4. Эквивалентная схема соединения трех конденсаторов с однородными диэлектриками между их пластин.

 

Общая ёмкость схемы С, расположенной на рис. 4 определяется из выражения:

.                                                                                                   (5)

Подставив параметры конденсаторов в выражение (5), получим:

.                                                                                       (6)

Из выражения (6) следует, что:

,                                                                                     (7)

где a, b, c – соответствующие расстояния между пластинами конденсаторов C₁, C₂, C₃ (рис 4), S – площадь их пластин.

Емкость конденсатора высчитывается по формуле:

,                                                                                                                  (8)

где l – расстояние между пластинами:

.                                                                                                               (9)

Из выражения (7) введем переменную m:

.                                                                                            (10)

Учитывая выражения (7)-(10) получим:

.                                                                                                     (11)

Остается лишь найти расстояния a, b, c, определив координаты точек на плоскости t (рис. 3), имеющие на плоскости z (рис. 2) координаты:

.

Используя выражение (4), получим координаты этих точек на плоскости t соответственно:

.

Следовательно:

,                                                                                                    (12)

,                                                                                                   (13)

.                                                                                                                         (14)

Подставив выражения (10),(12)-(13) в выражение (11), и учитывая, что:

,

где D_и1, D_и1 – диаметры изоляций соответственно, d - диаметр проводящей жилы, получим:

. (15)

Выражение (15) позволяет произвести разработать закон управления производства кабелей связи с парной скруткой.

 

Литература

 

1.                  Чостковский, Б. К. Структурный синтез оптимального управления обобщенными параметрами электрических кабелей связи // Вестник СамГТУ Сер. «Технические науки». Самара, 2007. №1. С. 54-57.

2.                  Миролюбов, Н. Н. Методы расчета электростатических полей. – М.: Наука, 1963.

 

Поступила в редакцию 27.03.2013 г.