Нелинейные колебания токонесущей ортотропной цилиндрической оболочки в магнитном поле

 

Индиаминов Равшан Шукурович,

кандидат физико-математических наук, доцент,

Каюмов Азиз Аслидинович,

магистрант,

Гуломов Аскар Исмоилович,

магистрант.

Самаркандский филиал Ташкентского университета информационных технологий. Узбекистан.

 

В работе построена нелинейная двумерная модель магнитоупругости токонесущей цилиндрической оболочки с учетом конечной ортотропной электропроводностью, магнитной и диэлектрической проницаемости. При этом предполагалось, что главные направления ортотропии свойств материала оболочки совпадают с направлениями соответствующих координатных осей, а также считалось, что ортотропное тело линейно относительно магнитных и электрических свойств. Получена связанная разрешающая система нелинейных дифференциальных уравнений, описывающая напряженно-деформированного состояния гибких токонесущих ортотропных цилиндрических оболочек, обладающей ортотропной электропроводностью, находящихся нестационарных силовых и электромагнитных нагрузок, а также сформулирована краевая задача.

Ключевые слова: оболочка, магнитное поле, магнитоупругость.

Бризер купить

У нас можно купить квартиру

aero-control.ru

Особенности и нюансы арт-обекта

особенности и нюансы арт-обекта

mymilica.ru

 

The nonlinear two-dimensional model of magnetoelasticity is constructed for the current-carrying orthotropic cylindrical shells with taking into account the finite orthotropic electrical conduction, magnetic and dielectric permeability’s. It is assumed that the directions of coordinate axes as well as that the orthotropic body is linear relative to its magnetic and electric properties. The coupled resolving system of nonlinear differential equations is obtained, which describes the stress-strain state of flexible current-carrying orthotropic cylindrical shells orthotropic electrical conduction under action of force and electromagnetic fields. The technique of solving the proposed class of problems is proposed.

Keywords: shell, magnetic field, magneto elasticity.

 

Введение. Учет взаимодействия механических, тепловых, электромагнитных, гравитационных и других указанных полей позволяет охватить более широкий класс задач механики твердого деформируемого тела, оценить границы применимости теорий, не учитывающих связанности полей, исследовать новые эффекты и явления.

Большой научный интерес к механике связанных полей вызван практическими потребностями. При создании целого ряда технических устройств, современных конструкционных материалов необходимо учитывать эффекты, обусловленные взаимодействием электромагнитных и температурных полей с механическими полями.

Значительное количество работ, в которых изучаются различные аспекты проблемы магнитоупругости, выполнены для линеаризованной по возмущению электромагнитного поля системы уравнений. В то же время решение ряда прикладных задач, связанных с рассмотрением внешних воздействий, требует более точного учета эффектов связанности полей на основе нелинейной системы уравнений магнитоупругости. К таким задачам относятся и задачи определения напряженно-деформированного состояния гибких токонесущих пластин и оболочек.

1. Уравнения магнитоупругости в лагранжевых переменных.

Пусть тело находится в магнитном поле, создаваемым как электрическим током в самом теле, так и источником, находящимся вдали от тела. Примем также, что тело служит проводником электрического тока (токонесущее тело), который подводится к торцам тела от внешнего источника. Предполагается, что сторонний электрический ток в невозмущенном состоянии равномерно распределен по телу (плотность тока не зависит от координат). Тело обладает конечной анизотропной электропроводностью и не обладает свойством самовольной поляризации и намагничиваемости.

Определим величины и запишем уравнения, которые характеризуют свойства электромагнитных полей. Пусть электромагнитное поле тела в эйлеровой системе координат характеризуется вектором напряженности электрического поля , вектором напряженности магнитного поля , вектором электрической индукции  и вектором магнитной индукции , а в лагранжевой системе координат характеризуется соответственно,, и .

Анализ электромагнитных эффектов возможен на основе системы уравнений Максвелла, совместно с материальными уравнениями, связывающими между собой векторы  и , и ,  и  которые в случае линейных изотропных сред имеют вид [12]:     

где -называются соответственно электрической и магнитной проницаемостями, - электрической проводимостью среды. Свойства сред характеризуются параметрами  и .

В зависимости от свойств параметров  и  различают следующие среды: линейные, в которых параметры  и  не зависят от величины электрического и магнитного полей, и        нелинейные, в которых параметры  и  (или хотя бы один из них) зависят от величины электрического или магнитного поля. Все реальные среды, по существу, являются нелинейными. Однако при не очень сильных полях во многих случаях можно пренебречь зависимостью  и  от величины электрического и магнитного полей и считать, что рассматриваемая среда линейна.

В свою очередь, линейные среды делятся на однородные и неоднородные, изотропные и анизотропные. Однородными называют среды, параметры  и  которых не зависят от координат, т.е. свойства среды одинаковы во всех ее точках. Среды, у которых хотя бы один из параметров  и  является функцией координат, называют неоднородными. Если свойства среды одинаковы по разным направлениям, то среду называют изотропной. Соответственно среды, свойства которых различны по разным направлениям, называют анизотропным. В изотропных средах векторы  и , а также  и  параллельны, в анизотропных средах они могут быть не параллельными. В изотропных средах параметры  и -скалярные величины. В анизотропных средах, по крайней мере, один из этих параметров является тензором. Отметим, что определение связей между величинами и , а также  и  конкретизирует модель среды.

При движении проводящего тела в магнитном поле или при изменении магнитного поля во времени в теле возникают индуцированные токи и обусловленные ими пондеромоторные силы Лоренца, что, в свою очередь, сопровождается деформацией среды и появлением волн напряжений.

Движение упругой среды в магнитном поле описывается совместной системой уравнений электродинамики медленно движущейся среды и уравнений динамической теории упругости с учетом пондеромоторных сил. Данная система уравнений является нелинейной за счет нелинейности соотношений обобщенного закона Ома и выражений для пондеромоторных сил.

Упругие среда являются таковыми, что начальные относительные положения частиц влияют на внутренние усилия (как механического, так и магнитного происхождения) всюду в теле в более поздние моменты времени. Поэтому при исследовании таких объектов удобно применять начальные координаты каждой частицы, т.е. лагранжевы координаты.

Осуществим переход от эйлеровой системы координат  к лагранжевой  с помощью зависимостей [7, 8, 10, 1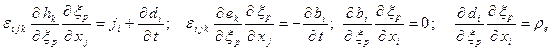1]:

 

 (1)

где через обозначена объемная плотность электрических зарядов.

Опуская промежуточные преобразования, уравнения Максвелла в лагранжевых переменных принимают вид [7, 11]:

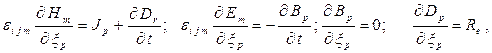      (2)

где        

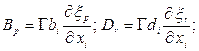
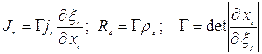.                                                               (3)

Уравнения движения материального тела, которые описывают их взаимодействие с электромагнитным полем, имеют вид [7]:

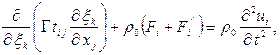                                                           (4)

где компоненты тензора напряжений Эйлера; плотность материала в недеформированном состоянии. Используя тензор напряжений Лагранжа

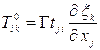,                                                                                                       (5)

уравнения движения запишем в виде

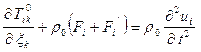.                                                                              (6)

В дальнейшем уравнение (10) также можно представить в виде

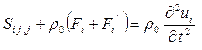.                                                                              (7)

где тензор напряжений, введенный в работе В.В.Новожилова [5].

В векторном виде уравнения магнитоупругости имеют вид [3, 7, 8, 9]:

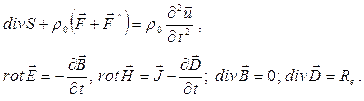                                      (8)

Соотношения (3) векторном виде запишем так:

                                    (9)

где . Обобщенный закон Ома

                                                                              (10)

а выражение для пондеромоторной силы Лоренца в материальных переменных запишем в виде

                                                            (11)

Таким образом, уравнения магнитоупругости в конечном виде запишем так:

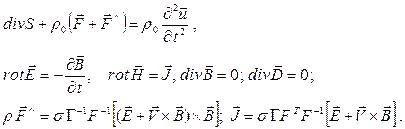                            (12)

Система уравнений (12) должна быть дополнена начальными условиями, граничными условиями и условиями на бесконечности [1, 7]. Отметим, что  и - операторы дивергенции ротора относительного неподвижного декартового базиса; - электрическая проводимость.

Систему уравнений магнитоупругости необходимо замкнут соотношениями, связывающими векторы напряженности и индукции электромагнитного поля, а также законам Ома, определяющим плотность тока проводимости в подвижной среде. Если анизотропное тело линейно относительно магнитных и электрических свойств, то определяющие уравнения для электромагнитных характеристик поля и кинематические уравнение для электропроводимости, а также выражения для сила Лоренца, с учетом стороннего тока  в переменных Лагранжа запишутся соответственно в виде [2, 6, 7, 9, 11]:

, ,

,                                                             (13)

 .

Отметим, что в уравнениях Максвелла пренебрегаем токами смещения, вектором электрической индукции и объемной плотностью электрических зарядов (квазистатическое поле); ,,-соответственно тензоры электрической проводимости, диэлектрической и магнитной проницаемости линейно анизотропного токонесущего тела .

Для однородных анизотропных сред они являются симметричными тензорами второго ранга [2, 4, 6, 9].

2. Уравнения магнитоупругости тонких анизотропных оболочек в нелинейной постановке.

При построении двумерных уравнений внутренней задачи магнитоупругости анизотропных оболочек в геометрически нелинейной постановке используем гипотезу Кирхгофа-Лява и адекватные ей электромагнитные гипотезы [1, 7].

Предлагаемая двумерная модель магнитоупругости задач теории анизотропных оболочек строится в квадратичном приближении, а в членах для сил Лоренца учитывается кубическая нелинейность. Это объясняется тем, что в данной постановке взаимодействие электромагнитного поля с полем деформаций осуществляется только за счет этих сил.

При изучении электродинамических уравнений движения теории анизотропных оболочек воспользуемся системой криволинейных координат  в относительной конфигурации тела. Рассматривая конечную трехмерную анизотропную оболочку в трехмерном евклидовом пространстве, ставим в соответствие каждой материальной точке тела координаты . Пусть  - радиус-вектор характерной частицы в данной конфигурации тела во время , и аналогично, обозначим через  радиус-вектор в фиксированной относительной конфигурации, которая является начальной. В этом случае, в рамках трехмерной теории, кинематические отношения представляются следующим образом:

; ; ;   

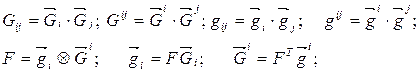                         (14)

где: ковариантные и контравариантные базовые векторы соответственно; - ковариантные и контравариантные метрические тензоры конфигурации в момент времени ;  соответствующие величины для начальной конфигурации; - дельта Кронекера; символ  - обозначает тензор процедуру. Суммирование по повторяющимся индексам не производится.

Принимая во внимание (14), векторы электромагнитных величин могут быть представлены следующими соотношениями:

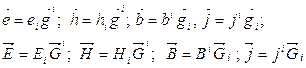                                                     (15)

Учитывая (1) и соотношения (14), получаем

          (16)

Выражения (16) устанавливают связь между электромагнитными величинами в лагранжевой и эйлеровой системах координат через метрику начальной и текущей конфигураций.

При построении двумерной теории тонких оболочек в геометрически нелинейной постановке воспользуемся уравнениями и соотношениями теории гибких оболочек в квадратичном приближении, с привлечением классической модели недеформируемых нормалей и гипотез электродинамики 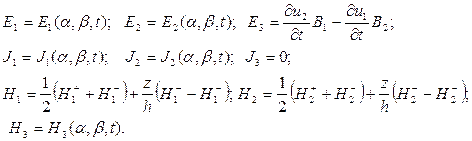[1, 7]:

                       (17)

Здесь  - компоненты пространственного вектора перемещений; - известные компоненты вектора напряженности магнитного поля на поверхностях оболочки. Соответствующая группа электродинамических гипотез является адекватной группе механических гипотез Кирхгофа-Лява теории гибких оболочек.

Для рассматриваемого случая квадратичной нелинейности [5, 7] деформации и углы поворота – величины малые, но вторые существенно превосходят первые. Выделенный бесконечно малый объемный элемент в процессе деформации изменит свое положение в пространстве (за счет смещения и поворота) и, кроме того, изменит свои размеры и форму. Учет малости удлинений и пренебрежение сдвигами по сравнению с углами поворотов позволяют не делать различия между размерами объемного элемента до и после деформации. Это дает возможность представить объемный элемент после деформации равным объемному элементу по деформации и отличающимся от него (геометрически) только своим положением в пространстве. Вышесказанное позволяет принять, что

 и

Здесь - элементарные площадки с нормалями  до деформации,  - та же площадка после деформации;  и - объемы элементарного элемента до и после деформации.

Такой подход позволяет учитывать нелинейность в соотношениях для деформаций, кривизн и кручения. При этом метрика оболочки остается практически недеформированной, так как радиусы кривизн и параметры Ламе соответствуют недеформированному состоянию оболочки. Отметим, что исходя из этих рассуждений, соотношения (6) приводятся к виду

                                                 (18)

Рассмотрим тонкий токонесущей круговой цилиндрической оболочки находящихся под действием нестационарных электромагнитных и механических нагрузок, пренебрегая влиянием процессов поляризации и намагничивания, а также температурными напряжениями считаем, что к торцу оболочку подводится переменный электрический ток от внешнего источника. Упругие свойства материала оболочки считаются ортотропными, главные направления, упругости которого совпадают с направлениями соответствующих координатных линий электромагнитные же свойства материала характеризуются тензорами электрической проводимости , магнитной проницаемости , диэлектрической проницаемости  .

При этом, исходя из кристаллофизики [6] и следуя работ [2, 4, 12], для рассматриваемого класса проводящих ортотропных сред с ромбической кристаллической структурой считаем, что тензоры , ,  принимают диагональный вид.

 В процессе деформации оболочки происходит изменение формы его поверхности, что приводит к изменению направления тока, то есть изменяется электромагнитное поле оболочки, возникают вихревые токи, которые, взаимодействуя с внешним магнитным полем, приводят к появлению сил электромагнитного происхождения, называемых силами Лоренца. Эти силы изменяют состояние тела и электромагнитное поле в нем.

Согласно результатам работ [3, 7, 10, 11], а также учитывая геометрию оболочки, полная система уравнений в криволинейной ортогональной системе координат позволяющая математически описать нелинейную двумерную модель магнитоупругости ортотропных цилиндрических оболочек, состоит из:

 уравнения движения

;

                                          (19)

;

;

;

уравнений Максвелла

;

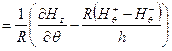;                             (20)

,

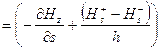выражений для деформаций

; ; ;

; ; ;                                            (21)

где ; .                                                                           (22)

соотношений упругости

 ; ;

; ;     (23)

 

Здесь   

Компоненты пондеромоторной силы имеют вид:

        

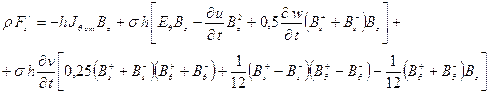
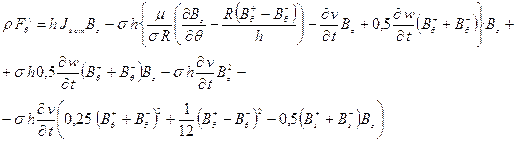
+                                               (24)

           

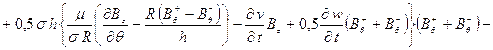
Здесь - нормальные тангенциальные усилия;  - сдвигающее усилие;  - поперечные усилия; - соответственно изгибающие и крутящий моменты; - компоненты перемещений; - составляющие напряженности электрического поля; -нормальная составляющая магнитной индукции; - известные составляющие магнитной индукции из поверхности оболочки. ,-составляющие плотности электрического тока от внешнего источника; -электрическая проводимость; - толщина оболочки; - модуль Юнга; - коэффициент Пуассона.

Приведенные уравнения отвечают квадратичной теории оболочек [6]. Составляющие силы Лоренца учитывают скорость деформирования оболочки, внешнее магнитное поле, величину и напряженность тока проводимости относительно внешнего магнитного поля. Учет нелинейности в уравнениях движения вызывает нелинейность в пондеромоторной силе.

Представим исходную систему уравнений в нормальной форме, разрешив их относительно производных по пространственной координате. В качестве разрешающих функций, выбираем  которые, будем также использовать при задании краевых условий.

После некоторых преобразований получаем систему нелинейных дифференциальных уравнений магнитоупругости в форме Коши, которая описывает напряженно–деформированное состояние токонесущей ортотропной цилиндрической оболочки при нестационарном воздействии механического и магнитного полей.

В векторном виде краевая задача имеет вид:

уравнения движения

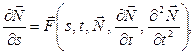
                                   (25)

граничные условия

                                                                (26)

начальные условия

 при                                                                                     (27)

Здесь: вектор столбец искомых функций; - в общем случае нелинейные вектор функции.

В дальнейшем, краевая задача (25), (26) с начальными условиями (27), решается численно в соответствии с методикой, изложенной в работах [7, 8, 10, 11].

Решение краевых задач магнитоупругости связано с существенными вычислительными трудностями. Это объясняется тем, что разрешающая система уравнений (25) является системой дифференциальных уравнений гипербола-параболического типа восьмого порядка с переменными коэффициентами. Предлагаемый подход к численному решению краевой задачи основывается на последовательном применении схемы Ньюмарка, метода квазилинеаризации и метода дискретной ортогонализации.

В заключение отметим следующее. Диэлектрические и магнитные свойства твердого тела изменяется не только при изменении плотности, но и при деформациях (сдвигах), когда плотность остается прежней. В результате деформации диэлектрические и магнитные свойства тела становятся анизотропными, а скалярные диэлектрическая и магнитная проницаемости заменяются тензорами второго ранга.

На основании полученных уравнений, с использованием предложенной методики, имеем возможность, учитывать как анизотропию материала, так и анизотропию внутреннего электромагнитного поля оболочки, а также влияние деформаций на электромагнитные свойства тела.

Такие задачи электромагнитоупругости весьма актуальны с точки зрений приложений. В случае тонких анизотропных или изотропных тел с анизотропной электропроводностью можно ставить и решать оптимальные задачи магнитоупругости путем вариации всех физико-механических параметров материала тела. В частности, при постоянных механических и геометрических параметрах задачи, с помощью изменения анизотропных электродинамических параметров можно получить конструктивные элементы с качественно новым механическим поведением.

 

Литература

 

1.                  Амбарцумян С.А., Багдасарян Г.Е., Белубекян М.В. Магнитоупругость тонких оболочек и пластин. М.: «Наука», 1977. - 272 с.

2.                  Багдасарян Г.Е., Данонян З.Н. Уравнения движения в перемещениях идеально-проводящих упругих анизотропных сред при наличии магнитного поля // Механика: Межвуз., сб., науч., тр., Мех., дефор., тверд., тела. - 1984. Вып. 3. - с. 32-42.

3.                  Индиаминов Р.Ш. Решение связанных динамических задач магнитоупругости токонесущих ортотропных конических оболочек // Сборник статьей Одиннадцатой междунар. научно-практ. конф. «Фундаментальные и прикладные исследования, разработка и применение высоких технологий в промышленности». 27-29 апреля 2011 г., г. Санкт-Петербург, Россия. Т. 3. - Санкт-Петербург, 2011. - С: 152-158.

4.                  Най. Дж. Физические свойства кристаллов и их описание при помощи тензоров и матриц. Изд-во «Мир», Москва 1967г. -275 с.

5.                  Новожилов В.В. Основы нелинейной теории упругости. – М.: Гостехиздат, 1948. -212 с.

6.                  Сиротин Ю.И., Шашкольская М.П. Основы кристаллофизики. – М.: «Наука», 1979г. -380 с.

7.                  Улитко А.Ф., Мольченко Л.В., Ковальчук В.Ф. Магнітопружність при динамічному навантаженні. К: Либідь, 1994. - 155 с.

8.                  Indiaminov R.SH. On the absence of the tangential projection of the Lorenz force on the ax symmetrical stressed state of current-carrying conic shells // International Journal Computational Technologies .- 2008.- Vol.13. N.6. P. 65 - 77.

9.                  Kaliski S. Wave equations of thermoelectromagnetoelasticity. Proc. Vibr. Probl. Pol. Acad. Sci., 1965, 6, № 3, 231-265- РЖ Мех, 1966б 6В133.

10.              Mol`chenko L.V., Loss. I.I., Indiaminov R.SH. The magnetoelastisity of conical shells mith ortotropic elektroconductivity in nonlinear position // Bulletin of the University of Kiev. Series: Physics & Mathematics.- 2007. N.2. P.85-90.

11.              Mol`chenko L.V., Loss. I.I., Indiaminov R.SH. Determining the Stress State of Flexible Orthotropic Shells of Revolution in Magnetic Field //International Applied Mechanics.-2008.-Vol. 44. No.8. P.882 - 891.

12.              Moon F.S. Magneto-solid mechanics. – N. –Y.: Wiley, 1984. - 437 p.

 

Поступила в редакцию 04.02.2013 г.