Расчет детских гравитационных аттракционнов

Расчет детских гравитационных аттракционнов

Гуць Виктор Степанович,

доктор технических наук, профессор,

Коваль Ольга Андреевна,

кандидат технических наук, доцент.

Национальный университет пищевых технологий, г. Киев, Украина.

Детская площадка предназначена для игр и активного отдыха, физического развития детей, прививает способность к активным играм, улучшает координацию движений. Повышение надежности, безопасности детских аттракционов на основе гравитационных спусков является основной задачей конструкторов, проектантов, эксплуатационников горок.

В статье рассмотрены и проанализированы режимы движения, силы, действующие на пользователей горок, аттракционов, разработаны математические модели на основе дифференциальных уравнений движения, определены скорости движения различных по размерам и поверхностным свойствам объектов, представлены функциональные зависимости, позволяющие выполнить расчеты отдельных элементов спуска.

Ключевые слова: расчет спуска, гравитационные спуски, уравнения движения, детские аттракционы.

Improving the reliability, safety of children's attractions based on gravitational descent is the main task of designers, planners, operatives.

The article describes and analyzes the modes of movement, forces acting on the user slides, rides, developed mathematical models - differential equations of motion, trajectory, speed of different size, shape and surface properties of the object allows you to perform calculations of individual elements of the shutter, its parameters in general.

Keywords: calculation of descent, gravity chutes, the equations of motion, children's attractions.

Вводная часть

Игра для ребенка является его потребностью, способствует развитию его интеллекта, речи, физического развития, обогащает фантазию, а совместные игры с другими детьми подготавливают его к социальной жизни в коллективе. Правильно спроектированные детские игровые площадки служат для обеспечения безопасных здоровых условий пребывания на свежем воздухе, физического развития, проведения досуга в коллективе сверстников. Наиболее привлекательным элементом детской площадки, как правило, является горка. Современные плавательные развлекательные комплексы обустраивают детскими горками-спусками. Скоростная горка как водная, так и безводная представляет собой гравитационный спуск, своеобразный гравитационный транспорт, осуществляющий движение посетителей под действием собственного веса по наклонному транспортирующему желобу линейного профиля, закругленного или подобного винтовому спуску. Задача конструкторов детских горок состоит в обеспечении надёжности, безопасности, экономической обоснованности эксплуатационных характеристик гравитационных спусков.

Цель работы – расчет параметров и режимов движения по гравитационному спуску на основе исследования скоростей и траекторий передвижения, обеспечения безопасности эксплуатации детских площадок, спусков, зон отдыха, аквапарков.

Объект исследования – движение материального объекта под действием гравитационных сил по наклонному спуску.

Методы исследований – математическое моделирование на базе диференциальных уравнений второго порядка с использованием методов символьной компьютерной математики, аналитические методы кинематических исследований параметров спуска.

Изложение основного материала исследования

Приоритетом разработки детских гравитационных спусков является безопасность их конструкции при условии достижения оптимальных конструктивных характеристик спусков.

В РФ [1], Украине [2] подготовлены стандарты, отвечающие европейским требования по безопасности для горкок, CSN EN 1176-3 – Playground equipment and surfacing – Part 3: Additional specific safety requirements and test methods for slides.

Горка представляет собой конструкцию с наклонной поверхностью скольжения, по которой ребенок спускается вниз под действием силы тяжести, конструктивно их разделяют на 3 участка: стартовый (А), скольжения (В), конечный или финишный (С) (рис. 1.).

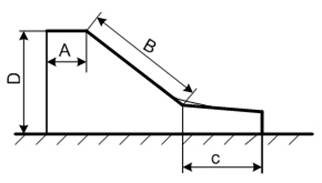
Рис. 1. Схема горки: А - стартовый участок; В - участок скольжения; С - конечный участок; D - высота горки.

Стартовый участок – часть горки, обеспечивающая доступ к участку скольжения, участок скольжения предназначен для спуска под действием силы тяжести, конечный участок обеспечивает торможение и остановку человека. Классифицируют горки в зависимости от возраста посетителей, назначения на: детские, семейные, экстремальные, водные и безводные. Требования к геометрическим параметрам участков скольжения детских горок зависят от возрастных категорий, общим является: средний угол наклона участка скольжения не должен превышать 40°, максимальный угол наклона – 60 °. Водная горка представляет собой водный аттракцион, имеющий наклонную поверхность скольжения, по которой пользователь движется под действием сил тяжести и инерции и где вода используется как среда, с помощью которой регулируется скорость движения и обеспечивается торможение и остановка пользователя в зоне финиша. Трасса спуска состоит из участков разгона и замедления. На основной части конструкции водной горки сформирована поверхность скольжения, которая определяет траекторию и скорость движения пользователя. Финишную часть может представлять участок спуска, переходящий в бассейн для падения или соскальзывания в воду. Гравитационные спуски для водных аттракционов характеризуют высотой, уклоном трассы спуска, средней и максимальной скоростью движения посетителя. В стандартах средняя скорость V_cp , движения объекта, рассчитывают по формуле: V_cp= B / t, где В – длина трассы спуска, м; t – время спуска по трассе. Как правило, расчет максимальных скоростей проводят в основном по эмпирическим зависимостям или упрощенным уравнениям движения, что влияет на их точность.

Расчет гравитационного спуска

Рассмотрим движение объекта (условного посетителя) на прямолинейном наклоненном участке гравитационного спуска. Считаем эту часть спуска прямым желобом, наклоненным под углом α к горизонту. Определим режим движения на этом участке.

Объект (условный посетитель) попадает на прямолинейную наклоненную поверхность с начальной скоростью V₁. На рис. 2 показана схема сил, действующих на объект массой m, который движется по наклоненному спуску под углом к горизонту .

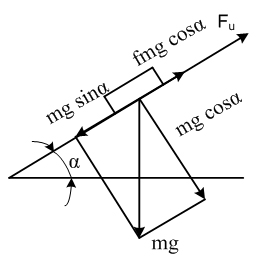
Рис. 2. Схема сил, действующих на объект, находящийся на прямолинейном наклоненном под углом к горизонту участке гравитационного спуска.

Дифференциальное уравнение движения для данного случая будет иметь вид:

, (1)

где - сила скатывающая; - сила инерции Ньютона, - сила трения; - путь скольжения; - коэффициент трения; m – масса объекта. Для случая, когда коэффициент трения не зависит от скорости передвижения , то решение уравнения (1) при начальных условиях t=0 , s(t)=0; ds/dt=V₁ представлено уравнением (2)

. (2)

Выполнив его дифференцирование, найдем скорость передвижения объекта скольжением:

. (3)

Из уравнений (2), (3), задавшись одной из трех неизвестных - углом наклона спуска α, длинной s пути скольжения, временем t скольжения, за которое объект массой сдвинется на расстояние , остановится, либо продолжит движение до остановки, можно найти две другие величины.

Как правило, конечная (финишная) часть спуска располагается горизонтально или под небольшим углом, остановка произойдет в случае V=0 или приближается к нулю. Тогда уравнение (3) представим в виде:

. (4)

Для малых углов примерно имеем . (5)

Для стартового участка, приняв во внимание, что V₁ =0, уравнения (2) и (3) будут иметь вид:

, (6)

(7)

Для гравитационных детских аттракционов, с точки зрения безопасности, наиболее важным является определение максимальной скорости движения и скорости движения в финишной точке, которая не должна превышать граничные величины или быть равной нулю. Описать движение с учетом ряда дополнительных факторов, например, таких как наличие сопротивления движению пропорционального скорости, можно записав уравнение (1) в виде:

, (8)

где k – коэффициент дополнительного сопротивления.

Коэффициент дополнительного сопротивления позволяет учитывать сопротивление воздуха, наличие, форму и влияние бортов желоба. Решение уравнения (8) при начальных условиях t = 0 => s(0)=0; V (0) = 0 (стартовый участок) представлено формулой 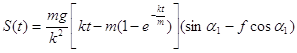(9):

(9).

Выполнив дифференцирование уравнения (9), найдем скорость движения

(10).

Задавшись массой ребенка, коэффициентами трения, сопротивления воздуха, из уравнения (10) можно определить: скорость скольжения в любой момент времени в зависимости от угла наклона спуска. Пример функциональной зависимости указанных параметров для ребенка массой 10 кг, при коэффициенте дополнительного сопротивления k=0,1 и трения =0,3, представлена на рис.3. Скорость скольжения изменяется от нуля до 14 м/с может достигать за время от 1 до 3 с в зависимости от угла наклона a (Рис. 3).

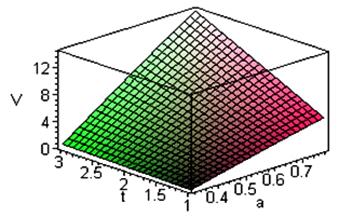
Рис. 3. Анализ функциональной зависимости скорости спуска (V) от угла наклона (a) участка скольжения и времени спуска (t).

Выводы

Полученные математические зависимости позволяют рассчитать геометрию безопасного спуска, что является обязательными для активного досуга детей.

Литература

1. ГОСТ Р 52168 – 2012 Оборудование детских игровых площадок. Безопасность конструкции и методы испытаний горок. Общие требования, от 18.09.2012. [Электронный ресурс]. – Режим доступа: http://dokipedia.ru/document/5155256. Получено 15.09.2014.

2. НПАОП 97.2–1.01–06 Правила будови і безпечної експлуатації атракціонної техніки від 01.03.2006.[Электронный ресурс]. – Режим доступа: http://otipb.at.ua/load/pravila_budovi_i_bezpechnoji_ekspluataciji_atrakcionnoji_tekhniki_npaop_92_7_1_01_06/2-1-0-1157. Получено 15.09.2014.

Поступила в редакцию 17.11.2014 г.