Альтернативная мера оценки рисков для финансовых рядов с помощью эффекта'Северо-Восточного ветра волатильности'
Пучков Андрей Александрович,
магистр экономики, докторант Рижского технического университета.
Andrejs Puchkovs,
Economist, Mg. oec., PhD student of Riga Technical University.
This paper illustrates alternative indicator for risk estimation. This indicator is beneficial for financial market instability prediction on early stages. Alternative risk measure is based on North-East Volatility Wind Effect and its helical (spiral) structure investigation in frequency domain. North-East Volatility Wind effect is described in [6-10]. but helical structure exploration is made in article “North-East Volatility Wind Effect in Traveling Wave Perspective. Helical Structure of Volatility wave Fourier Coefficients” which is expected publication in current journal.
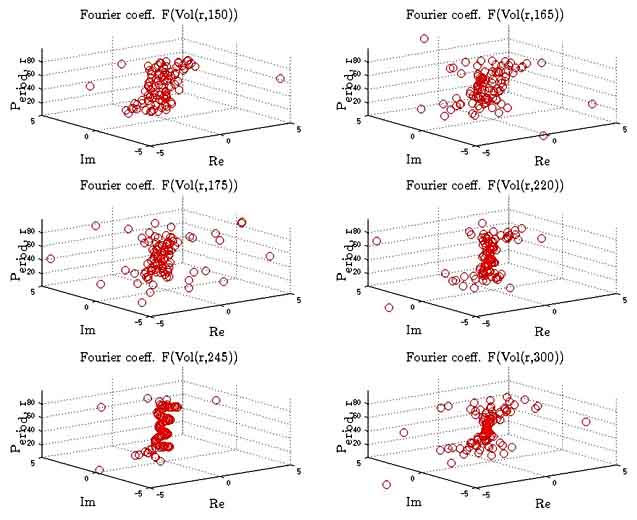
Fig. 1. Volatility pie function representation in frequency domain. Evolution in time.
In
this article “North-East Volatility Wind Effect in Traveling Wave Perspective.
Helical Structure of Volatility wave Fourier Coefficients” evolution of
'Volatility pie' function in a frequency domain![]() is considered. The same picture is obtained for
is considered. The same picture is obtained for ![]() function. Results are represented
next.
function. Results are represented
next.
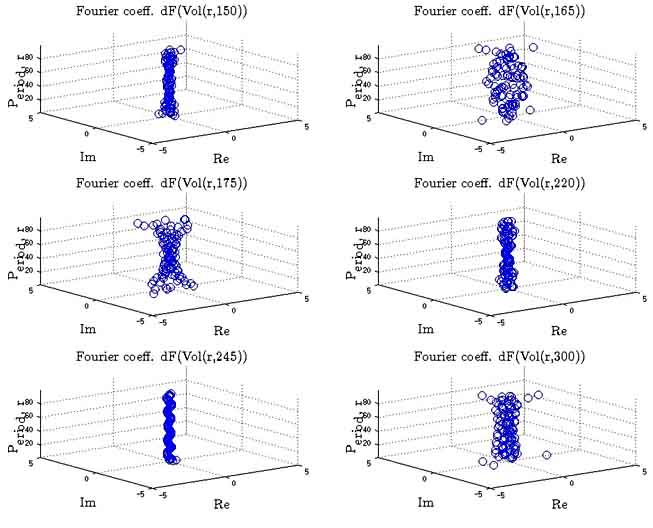
Fig.
2. Volatility pie ![]() function representation in
frequency domain. Evolution in time.
function representation in
frequency domain. Evolution in time.
According
to results volatility pie in frequency domain and![]() did not have clear structure. The same conclusions
are done about function
did not have clear structure. The same conclusions
are done about function![]() .But in time
.But in time ![]() (during financial crisis 2007
peak) the picture has been changing and functions a
(during financial crisis 2007
peak) the picture has been changing and functions a![]() and
and![]() acquired clear helical (spiral)
structure. This effect is explored by less number of explicit harmonics
(harmonics with higher magnitude). [13] After market crisis 2007, clear clear
helical (spiral) structure was lost.
acquired clear helical (spiral)
structure. This effect is explored by less number of explicit harmonics
(harmonics with higher magnitude). [13] After market crisis 2007, clear clear
helical (spiral) structure was lost.
Since
Fourier transform is done for investigated volatility wave ![]() which is fixed in time
which is fixed in time ![]() , obtaining
, obtaining ![]() (while
(while ![]() ), helical structure 'regularity' can be measured as
a minimal total distance between Fourier coefficients
), helical structure 'regularity' can be measured as
a minimal total distance between Fourier coefficients ![]() (from spiral), since
(from spiral), since ![]() is a three dimensional function.
is a three dimensional function.
![]() (1)
(1)
Minimal
total distance is calculated as a total distance, which includes (spiral) chain
of all Fourier coefficients, which belongs to ![]() . Next Fourier coefficient is included in chain, if
it is located in minimal distance to previous Fourier coefficient. Procedure is
repeated until the last Fourier coefficient is included in spiral chain.
. Next Fourier coefficient is included in chain, if
it is located in minimal distance to previous Fourier coefficient. Procedure is
repeated until the last Fourier coefficient is included in spiral chain.
This procedure could be simplified by (2) equation.
![]() (2)
(2)
The
smaller distance ![]() , more regularity in helical
(spiral) structure. Acquired
, more regularity in helical
(spiral) structure. Acquired ![]() measure is calculated for all
time variables
measure is calculated for all
time variables ![]() , obtaining
, obtaining ![]() function which is used as
alternative risk measure.
function which is used as
alternative risk measure.
In
the next figure calculation results of alternative risk measure ![]() are shown comparing with
volatility measure (logarithmic variance indicator). Results are illustrated on
the Dow Jones Industrial Index data.
are shown comparing with
volatility measure (logarithmic variance indicator). Results are illustrated on
the Dow Jones Industrial Index data.
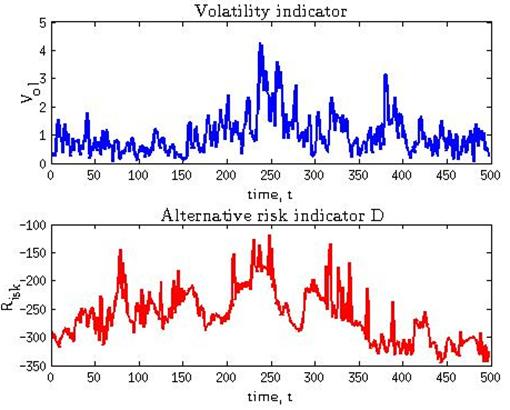
Fig. 3 Volatility indicator and
alternative risk indicator![]() .
.
The dynamics of analyzed indicators are visually very similar, but correlation in fact is not high (30%).
The
main question to be answered how alternative risk indicator ![]() could be used for volatility
forecasting. In order to answer this question consider early forecasting task
by using alternative risk indicator
could be used for volatility
forecasting. In order to answer this question consider early forecasting task
by using alternative risk indicator ![]() . Future volatility indicator is forecaster in 100
time units (about~100 weeks) by using Alternative risk indicator
. Future volatility indicator is forecaster in 100
time units (about~100 weeks) by using Alternative risk indicator ![]() in past. For forecasting NARX
(Nonlinear AutoRegressive with External Input) neural network with following
architecture.
in past. For forecasting NARX
(Nonlinear AutoRegressive with External Input) neural network with following
architecture.
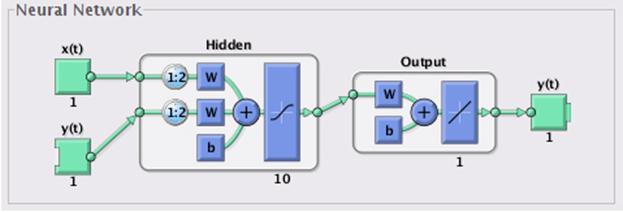
Fig. 4. NARX Neural Network architecture.
This network is trained on 70% of data, validated on 15% and tested on 15% of data. After 7-th epoch, the best best result is obtained on validation set. Trained Network provides output with following dynamics.
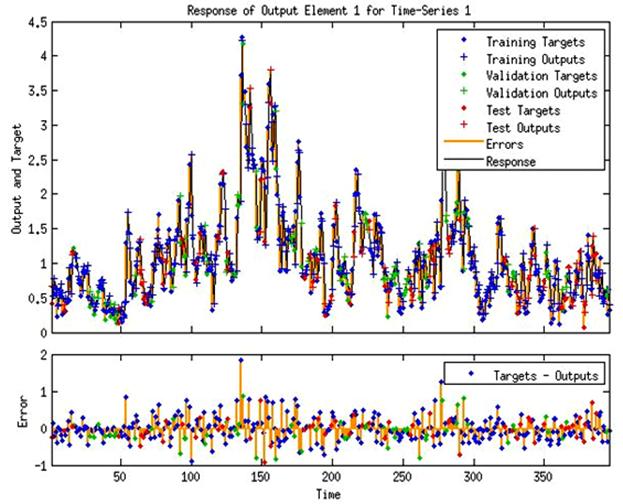
Fig. 5. NARX Neural Network output dynamics.
Output provided by network is highly correlated with Target. But results could be improved. implementing input data decomposition. Overall forecasting results are not bad. Output-Target regression data are shown in next figure.
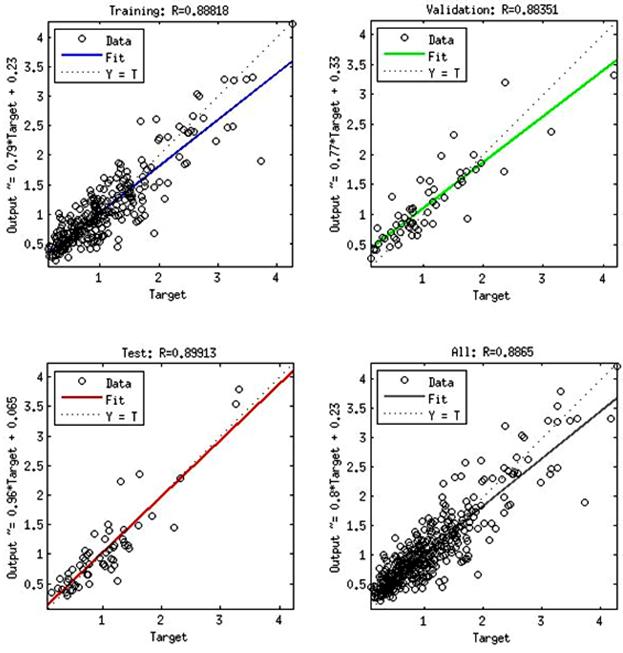
Fig. 6. NARX Neural Network output - target regression.
The following R/MSE results are acquired:
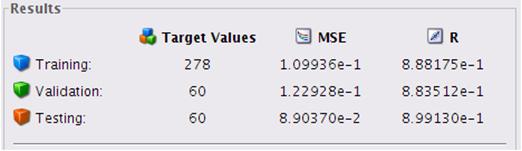
Fig. 7. NARX Neural Network result estimation.
For
estimated Neural Network, Target and Output correlation on Test, Validation and
Testing observations are about 90%, MSE indicator is small. According research
Alternative risk indicator ![]() obtained from distance between
'helical' Fourier coefficients could be used for Volatility indicator
forecasting for about 100 weeks, but algorithm modification could be used for
better forecast.
obtained from distance between
'helical' Fourier coefficients could be used for Volatility indicator
forecasting for about 100 weeks, but algorithm modification could be used for
better forecast.
Bibliography
1. BASU, T. K. Lecture Series on Digital Signal Processing. IIT Kharagpur, 2013, 555 s.
2. BURNAEV Primenenije vejvlet preobrazovanija dla analiza signalov. MFTI, 2007, ISBN 5-93517-103-1, 138 s.
3. CAPINSKI, M., T., Z. Mathematics for Finance An Introduction to Financial Engineering.Springer, 2010, 309 s.
4. GADRE, V. M. Lecture series in Multirate Digital Signal Processing and Multiresolution analysis. IIT Bombay, 2013, 555 s.
5. JAKOVLEV, A. N. Vvedenije v vejvlet preobrazovanija. NGTU, 2003, ISBN 5-7782-0405-1,576 s.
6. PUČKOVS, A. Equity Indexes Analysis and Synthesis by Using Wavelet Transform. In: 7th International Conference on Computational and Financial Econometrics (CFE 2013): Programme and Abstracts, United Kingdom, London, 13-16 December, 2013. Birkbeck: University of London, 2013, pp.98-98.
7. PUČKOVS, A. Stock Indexes Volatility Evolution Research in Volatility Layers. Журнал научных публикаций аспирантов и докторантов, 2014, Nr5(95) Mai2014, pp.32-37. ISSN 1991-3087.
8. PUČKOVS, A. Computational Aspects of 'North-East Volatility Wind Effect'. Журнал научных публикаций аспирантов и докторантов, 2014, Nr5(95) Mai2014, pp.261-274. ISSN 1991-3087.
9. PUČKOVS, A. Stochastic Process, Based on North-East Volatility Wind Effect. Журнал научных публикаций аспирантов и докторантов, 2014, Nr5(95) Mai2014, pp.220-226. ISSN 1991-3087.
10. PUČKOVS, A., MATVEJEVS, A. ’North-East Volatility Wind’ Effect. In: 13th Conference on Applied Mathematics (APLIMAT 2014): Book of Abstracts: 13th Conference on Applied Mathematics (APLIMAT 2014), Slovakia, Bratislava, 4-6 February, 2014. Bratislava: 2014, pp.67-67. ISBN 9788022741392.
11. PUČKOVS, A., MATVEJEVS, A. ’Northeast Volatility Wind’ Effect. Aplimat Journal, 2014, Vol.6, pp.324-328. ISSN 1337-6365.
12. SMOLENCEV Osnovi Teoriii Vejvletov v MATLAB. DMK Press, 2005, ISBN 5-94074-122-3,304 s.
13. Fourier series. Introduction. liraeletronica.weebly.com [http://liraeletronica.weebly.com/uploads/4/9/3/5/4935509/introduction_fourier_series.pdf] (Accesed 01. July 2014).
14. Fourier_series. Wikipedia.org. [http://en.wikipedia.org/wiki/Fourier_series], [http://en.wikipedia.org/wiki/Fourier_series#mediaviewer/File:Fourier_series_square_wave_circles_animation.gif] (Accesed 01. July 2014).
Поступила в редакцию 11.07.2014 г.