Компьютерная система программного задания поперечной подачи шлифовального круга

 

Еникеев Александр Фанилович,

доцент,

Абрамская Инна Богдановна,

старший преподаватель,

Яровой Роман Александрович,

старший преподаватель.

Украинский государственный университет железнодорожного транспорта, Краснолиманский филиал.

 

Введение

 

При разработке средств автоматизации технологических процессов алмазного шлифования (АШ) нашел применение метод программного задания поперечной подачи шлифовального круга (ШК) [1]. Реализация этого метода одномерной компьютерной системой (КС) сокращает на 20% время обработки детали и обеспечивает получение заданного «квалитета» чистоты обработанной поверхности.

Целью статьи является разработка одномерной КС программного задания поперечной подачи шлифовального круга (ШК) и анализ эффективности ее аппаратных средств. Достижение поставленной цели достигается путем решения следующих задач:

·                    разработка концепции структурно-логической организации одномерной КС программного задания поперечной подачи ШК;

·                    математическое моделирование блоков КС;

·                    синтез устройства обработки сигнала поперечной подачи ШК;

·                    анализ эффективности КС.

 

Методика синтеза аппаратных средств

 

Она состоит из таких вычислительных процедур:

·                    моделируем функциональные блоки КС в виде передаточных функций ;

·                    в результате статистической обработки экспериментальных данных с использованием информационного подхода устанавливаем полосу нечувствительности первичного преобразователя вокруг номинальной характеристики преобразования ;

·                    в результате анализа структурно-логической схемы КС и математических преобразований определяем его передаточную функцию ;

·                    исследуем передаточную функцию. При этом определяем ее нули и полюсы, запас устойчивости по амплитуде и фазе, строим частотные характеристики. В результате получаем упрощенное выражение для передаточной функции;

·                    моделируем помехи КС и посредством методики суммирования случайных составляющих устанавливаем полосу неопределенности выходного сигнала;

·                    представляем входной сигнал КС ограниченным рядом Фурье;

·                    решение задачи Коши для обыкновенных дифференциальных уравнений, которые описывают динамику аппаратно-программных средств, существенно упрощается применением преобразования Лапласа. Выходной сигнал КС получается согласно теореме о свертке. Для его вычисления применим обратное преобразование Лапласа к выражению для передаточной функции;

·                    определяем дискретную передаточную функцию КС ;

·                    в качестве эталонной модели при синтезе устройства цифровой обработки используем выходной сигнал;

·                    строим имитационную модель и устанавливаем эффективность КС.

 

Моделирование элементов КС

 

Разработку одномерной КС выполним на основе метода непосредственного цифрового управления с использованием микроконтроллера и метода отработки рассогласований между оптимальными значениями подач ШК, которые хранит банк данных, и их измеренными значениями. Структурно-логическое построение одномерной КС программного задания поперечной подачи ШК представлена на рис. 1. На этом рисунке обозначено: Д – датчик положения, П – преобразователь, ЭП – электрический привод, ИМ – исполнительный механизм. Выполним моделирование блоков КС.

 

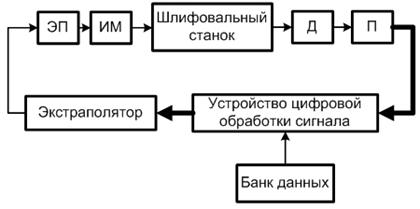
Рис. 1. Структурно-логическое построение КС.

 

Привод поперечной подачи ШК снабжен устройством для измерения линейных перемещений в виде фотоэлектрической линейки LS-101. Это устройство формирует синусоидальный выходной сигнал, количество периодов которого определяет величину поперечной подачи на текущий проход ШК. Чувствительность фотоэлектрической линейки LS-101, которая используется для измерений, составляет 0.1 мкм. В динамическом отношении блок Д представим пропорциональным звеном с некоторой полосой нечувствительности вокруг его номинальной характеристики преобразования [2].

Блок П состоит из таких функциональных модулей: преобразователь синусоидального сигнала в импульсный, который выполнен на базе транзисторного ключа; десятиразрядный счетчик импульсов, который обнуляется после считывания информации устройством цифровой обработки сигнала. Специфика работы этого блока позволяет представить его апериодическим звеном с известным запаздыванием [2]

,                                                                                                    (1)

 

где  – соответственно коэффициент передачи, запаздывание и постоянная времени блока П.

С учетом полосы  нечувствительности Д вокруг номинальной характеристики преобразования имеем такую передаточную функцию

.                                                                                                (2)

 

Работа цифроаналогового преобразователя (ЦАП) организована в соответствии с принципом «удержания», то такое устройство является экстраполятором нулевого порядка. Выходной сигнал экстраполятора нулевого порядка является ступенчатым. Тогда импульсная передаточная функция ЦАПа является реакцией на дельта-функцию единичной площади при нулевых начальных условиях

.                                                                                                            (3)

Из работы [3] известно, что

.

Тогда с учетом выражения (3) имеем

.                                                                                                    (4)

 

ВБ выполняет линейные операции, которые связаны с дифференцированием, интегрированием, сложением и т.п., то его можно представить линейным импульсным фильтром. В составе ВБ всегда имеется запоминающее устройство, которое позволяет помимо текущих значений входных и выходных сигналов учитывать их прошлые состояния. Поэтому если нужно учесть n значений выходного и m прошлых значений входного сигналов, то некоторый произвольный линейный алгоритм работы ВБ описывается так

, (5)

 

где е, е₁ – входной и выходной импульсные сигналы блока ВБ; τ_r – период решетчатой функции; δ – дельта-функция Дирака; а_v и b_μ – заданные постоянные коэффициенты.

Выполним над левой и правой частями соотношения (5) преобразование Лапласа при нулевых начальных условиях. Согласно определению (2.1) работы [3] и теоремы запаздывания, получим

.

 

Отсюда, обобщенная передаточная функция ВБ как некоторого произвольного цифрового фильтра имеет такой вид

.

 

 

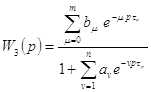Наиболее общий случай представления передаточной функции ВБ имеет место, когда m = 1, n = 0, b₀ = τ_r^-1 и b₁= -τ_r^-1. В этом случае последнее выражение приобретает такой вид

.                                                                                                   (6)

 

Привод поперечной подачи ШК без потери точности представим такой передаточной функцией [2]

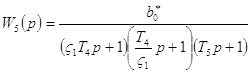.                                                                   (7)

 

 

Анализ модели КС

 

Структурно-логическое построение математической модели КС представлена на рис. 2. Банк данных процесса АШ хранит величины поперечной подачи ШК в виде оптимальных углов поворота ИМ. Выполним анализ этой схемы с целью получения выражения для передаточной функции.

 

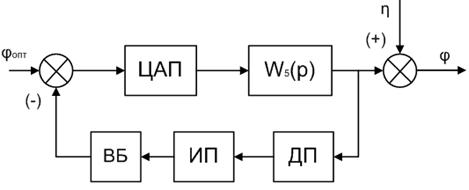
Рис. 2. Структурно-логическое построение модели КС.

 

Динамические особенности работы блоков ДП и ИП в составе КС позволяют представить их пропорциональным звеном с запаздыванием [2]. Передаточная функция такого звена имеет вид

,                                                                                                      (8)

где  – коэффициент усиления выбираем из условия нормирования,  – запаздывание.

Передаточная функция КС после математических преобразований получена в таком виде

,                                                           (9)

 

 

где , ,

, .

 

Частотные характеристики КС представлены на рис. 3. При получении входного сигнала КС учтем следующее:

-                   во время прямого и обратного хода ШК фаза выходной величины изменяется на 180⁰;

-                   прямой и обратный ход образуют период основной гармоники частотного представления входной величины.

С учетом вышеизложенного такой сигнал наиболее полно соответствует специфике поставленной задачи

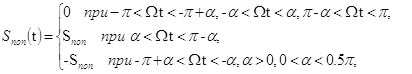                           (10)

 

 

где , t₂ – время взаимодействия ШК с обрабатываемой поверхностью детали.

 

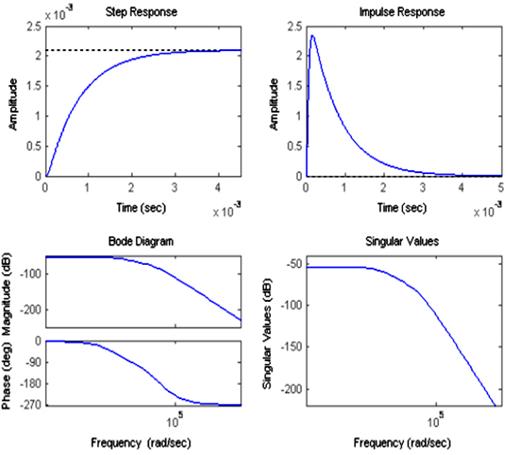
Рис. 3. Результаты исследований КС.

 

Разложение сигнала (10) в ряд Фурье имеет следующий вид

.                                 (11)

 

Преобразуем последнее выражение путем замены гармонических составляющих суммой экспоненциальных сигналов

,                                                      (12)

 

где .

 

 

Для вычисления интеграла свертки применим обратное преобразование Лапласа к уравнению (9). После преобразований имеем такое выражение

,                                                                                                   (13)

где .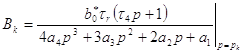

 

 

Расчет корней характеристического уравнения передаточной функции (9) дал такие результаты:

ans = 1.0e+004 *

 -4.5731

 -3.6239

 -2.4529

 -0.1339

Интеграл свертки на основе выражений (12) и (13) дал уравнение, которое описывает динамику выходного сигнала КС

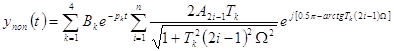.                              (14)

 

 

Для вычисления дискретной передаточной функции привода поперечной подачи ШК раскладываем выражение (7) на простые дроби. Дискретная передаточная функция привода после преобразований получилась в виде отношения двух степенных полиномов

,                                                            (15)

 

где      ,       ,               ,

;

;

; ;

; ; .

 

Блоки П, устройство цифровой обработки сигнала и ЭП вносят запаздывание в работу КС. Будем считать, что дискретное время запаздывания КС по входному сигналу, равное сумме запаздываний указанных блоков, составляет 2Т₀. Соответственно порядок модели КС составляет d=3. С учетом этого запаздывания дискретная передаточная функция привода получилась в виде

.                                   (16)

 

Дискретная передаточная функция по возмущению после преобразований получилась в виде отношения двух степенных полиномов

.                                                                (17)

 

 

Синтез устройства цифровой обработки сигнала

 

В основу разработки этого устройства положен метод синтеза на базе эталонной модели КС. Закон отработки входного сигнала КС на основе использования эталонной модели имеет такой вид

,                                                                          (18)

где  – сигнал поперечной подачи ШК в дискретные моменты времени ;  – полиномиальные выражения относительно оператора сдвига, а именно

,                                                               (19)

,                                                                  (20)

.                                                                (21)

Процедура синтеза устройства цифровой обработки сигнала сведена к задаче определения параметров полиномов ,  и  таким образом, чтобы основной контур был устойчивым. Реакция этого контура на изменение входного сигнала определяется эталонной моделью КС. Уравнение эталонной модели имеет вид

.                                                                                              (22)

 

Цель КС ликвидация ошибки рассогласования. Для этого нужно подобрать многочлен  такой, чтобы выполнялось такое равенство

.                                                                                     (23)

де  – стохастическая помеха, которая действует на выходной сигнал.

Полином  определяет динамику переходного процесса основного контура при устранении ошибки рассогласования. Поскольку величиной погрешности  можно задаться, а ширина  интервала неопределенности определена, то полином  приобретает вид

.                                                                                   (24)

 

Полином  представим в виде

, где .                   (25)

 

Характеристическое уравнение, которое определяет динамику основного контура, будет равняться полиному , то есть

.                                                                       (26)

 

С учетом этого дискретная передаточная функция основного контура КС примет вид

.                                                                                                 (27)

 

Задача аппаратно-програмных средств состоит в обеспечении соответствия выходных сигналов эталонной модели (22) и основного контура (27) на изменение входного сигнала. Следовательно, можно приравнять правые части этих уравнений. В результате получим следующее выражение

.                                                                                         (28)

 

Отсюда, после преобразований имеем такое выражение

,                                                                (29)

где , , , .

 

Выполним синтез устройства цифровой обработки сигнала поперечной подачи ШК в условиях действия помех. Запишем прогнозируемое значение выходной координаты привода

.                                                                                                (30)

 

Определим из последнего выражения входной сигнал и подставим его в уравнение (18). После этого уравнение отработки входного сигнала КС примет такой вид

.                                                                      (31)

Принимая во внимание то, что , уравнение отработки входного сигнала КС запишем в виде

.

 

Выходной сигнал КС на ИМ поперечной подачи ШК имеет вид

.                                                   (32)

 

где .

 

Представим входной сигнал КС в виде единичной функции, которая имеет амплитуду . Соответственно этот сигнал в форме z-преобразования имеет вид

.                                                                                                              (33)

 

Для установившегося режима работы устройства цифровой обработки сигнала (ошибка рассогласования равняется нулю) имеем

.                                                                                              (34)

 

После подстановки в это уравнение выражения (33) и преобразований получим полином  в таком виде

,                                                                                    (35)

где      ,            ,    .

 

При отсутствии входного сигнала из выражения (18) имеем

.                                                                                           (36)

С учетом того, что , имеем такое уравнение

.

Отсюда, после преобразований получен полином  в виде

,                                                                                               (37)

где его коэффициенты имеют такие значения

,                    ,

 

.

 

 

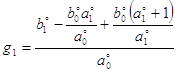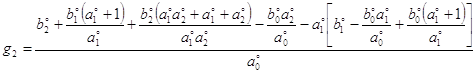Получим передаточную функцию устройства цифровой обработки сигнала поперечной подачи ШК. Из выражения (31) с учетом уравнения (30) после преобразований имеем

.                                                                          (38)

 

Отсюда, после замены  и преобразований получим передаточную функцию устройства цифровой обработки сигнала в таком виде

.                                                                     (39)

 

После подстановки коэффициентов полиномов , ,  и  в выражение (39) и преобразований получим передаточную функцию устройства цифровой обработки сигнала в таком виде

.                                                 (40)

 

На основе выражений (16), (17), (25), (29), (35), (37) и (40) собрана имитационная модель КС (рис. 4).

 

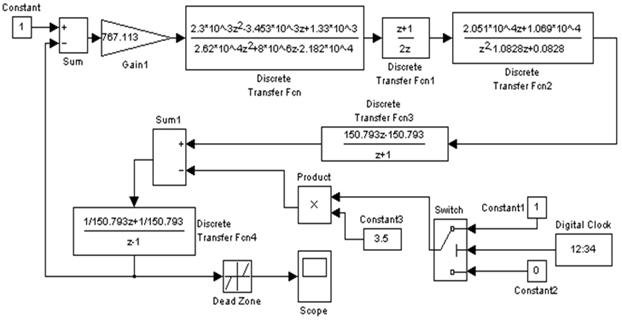
Рис. 4. Имитационная модель КС.

 

Выводы

 

На основе метода отработки рассогласований между измеренными значениями подач ШК и их оптимальными значениями, которые хранит банк данных процесса АШ, построена архитектура КС. В результате анализа структурно-логической схемы с использованием дискретного преобразования Лапласа построена эталонная модель КС. На основе минимизации квадратичного критерия качества с использованием эталонной модели КС синтезировано устройство цифровой обработки сигнала поперечной подачи ШК. Построена имитационная модель КС. В результате имитационного моделирования установлено, что время отработки входного сигнала составило 0.04 с, что удовлетворяет требованиям по производительности КС. Вид выходного сигнала - колебательный. Программное задание поперечной подачи происходит во время пауз между прямым и обратным ходом ШК. Соответственно, переколебания выходного сигнала не оказывают влияния на точность задания.

 

Литература

 

1.                  Еникеев А.Ф. Оптимальное управление технологическим процессом алмазного шлифования. – Краматорск: ДГМА, 2001. – 160 с.

2.                  Синтез цифрового регулятора поперечной передачи шлифовального круга / Еникеев А.Ф., Зыков И.С. // Вестник Национального технического университета «ХПИ». –Харьков: №57, 2008.– С. 87–93.

3.                  Микропроцессорные автоматические системы регулирования. Основы теории и элементы: Учебное пособие / [Гл. ред. В.В. Солодовников]. – М.: Высшая школа, 1991. – 255 с.

 

Поступила в редакцию 11.11.2014 г.