О сравнении по ненулевому рациональному модулю применительно к теореме Ферма
Карпунин Иван Иванович,
доктор технических наук, профессор, профессор кафедры Белорусского национального университета, академик МИА и МАИТ.
ТЕОРЕМА 1. Число регулярных простых чисел бесконечно. В литературе имеются данные о том, что количество простых чисел бесконечно [1,2]
Пусть ![]() – произвольная конечная система
иррегулярных простых чисел. Теорема будет доказана, если мы найдем иррегулярное
простое число
– произвольная конечная система
иррегулярных простых чисел. Теорема будет доказана, если мы найдем иррегулярное
простое число
![]() ,
,
отличное от ![]() . Где
. Где ![]() –
регулярное простое;
–
регулярное простое; ![]() – сомножитель (дробное число>1);
– сомножитель (дробное число>1);
![]() выбрано таким образом, что
выбрано таким образом, что ![]() >
>![]() .
. ![]() – число числителя чисел Бернулли,
– число числителя чисел Бернулли, ![]() – произведение регулярного числа
– произведение регулярного числа ![]() на
на ![]() ;
; 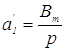 , где
, где ![]() –
целое число, полученное при делении числителя чисел Бернулли на иррегулярное
число, т. е.
–
целое число, полученное при делении числителя чисел Бернулли на иррегулярное
число, т. е. ![]() ;
; ![]() (
(![]() если не сокращать числитель и
знаменатель).
если не сокращать числитель и
знаменатель).
Предположим ![]() .
.
Так как для
числа Бернулли ![]() мы имеем [1]
мы имеем [1]
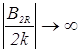 при
при ![]()
то при
достаточно большом натуральном ![]() рациональное число
рациональное число ![]() будет по абсолютной величине >1.
будет по абсолютной величине >1.
Пусть ![]() – простое число, входящее в его числитель
(при несократимой записи). Если бы
– простое число, входящее в его числитель
(при несократимой записи). Если бы ![]() , то по теореме
Штаудта [1], число
, то по теореме
Штаудта [1], число ![]() входило бы в знаменатель
входило бы в знаменатель ![]() , а это не по выбору числа
, а это не по выбору числа ![]() . Следовательно,
. Следовательно, ![]() не
делит
не
делит ![]() , а поэтому
, а поэтому ![]() отлично
от
отлично
от ![]() (и от 2). Обозначим через
(и от 2). Обозначим через ![]() остаток от деления
остаток от деления ![]() на
на ![]() , так
что
, так
что ![]() . Отсюда следует, что
. Отсюда следует, что ![]() – четное и
– четное и ![]()
Вместе с ![]() число
число ![]() также
не делится на
также
не делится на ![]() . Воспользовавшись сравнением
Куммера [3-5], получим в кольце
. Воспользовавшись сравнением
Куммера [3-5], получим в кольце ![]() – целых рациональных
чисел сравнение
– целых рациональных
чисел сравнение ![]() , поэтому
, поэтому ![]()
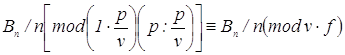 .
.
Для
обоснования разложения иррегулярного простого числа ![]() на
произведение двух простых сомножителей регулярного простого числа
на
произведение двух простых сомножителей регулярного простого числа ![]() на сомножитель
на сомножитель ![]() >1
(дробное число >1). Докажем следующую вспомогательную теорему.
>1
(дробное число >1). Докажем следующую вспомогательную теорему.
2. Вспомогательная
теорема. Если натуральное нечетное составное число ![]() является
произведением двух простых натуральных чисел
является
произведением двух простых натуральных чисел ![]() и
и ![]() (
(![]() ) (1),
то оно также является произведением третьего простого натурального нечетного
числа
) (1),
то оно также является произведением третьего простого натурального нечетного
числа ![]() на дробное число
на дробное число ![]() >1
(
>1
(![]() ). Если
). Если ![]() или
или ![]() равно 1, то имеем частный случай
равно 1, то имеем частный случай ![]()
![]() –
простое число (
–
простое число (![]() ).
).
Для
доказательства заметим, что 1 делит любое натуральное, поэтому достаточно предположить,
что ![]() >1. Тогда
>1. Тогда ![]() >
>![]() . Кроме того, также предположим, что
равенство (1) выполняется при
. Кроме того, также предположим, что
равенство (1) выполняется при ![]() , т.е.
, т.е. ![]() ;
; ![]() ;
; ![]() , где s' – простое число
, где s' – простое число ![]() .
.
Поскольку ![]() >1, для числа
>1, для числа ![]() имеется
предшествующее. Обозначим его
имеется
предшествующее. Обозначим его ![]() . Оно может удовлетворять
или не удовлетворять условию
. Оно может удовлетворять
или не удовлетворять условию ![]() >
>![]() . Если оно ему удовлетворяет, то для него
имеется предшествующее, которое мы обозначим
. Если оно ему удовлетворяет, то для него
имеется предшествующее, которое мы обозначим ![]() .
Тогда условие
.
Тогда условие ![]() >
>![]() может
выполняться или не выполняться.
может
выполняться или не выполняться.
Повторение
этого процесса привело бы к бесконечно убывающей последовательности чисел, если
бы мы на некотором этапе не получили числа ![]() в
числителе (как предшествующее предшествующему числу
в
числителе (как предшествующее предшествующему числу ![]() ), для
которого
), для
которого ![]() не больше
не больше ![]() . Но
. Но ![]() >
>![]() .
Таким образом, на основании принципа бесконечного понижения (спуска), такое
число
.
Таким образом, на основании принципа бесконечного понижения (спуска), такое
число ![]() найдется. Тогда либо
найдется. Тогда либо ![]() , либо
, либо ![]() <
<![]() . Если
. Если ![]() , то
, то ![]() в числителе равно
в числителе равно ![]() в знаменателе и случай 1 доказан.
в знаменателе и случай 1 доказан.
Если же ![]() <
<![]() , то
, то ![]() для некоторого
для некоторого ![]() .
Так как
.
Так как ![]() >
>![]()
![]() >
>![]() , то
отсюда следует, что
, то
отсюда следует, что ![]() >
>![]() .
Наконец, если
.
Наконец, если ![]() ; где
; где ![]() <
<![]() , то
, то ![]() , иначе
, иначе
![]() <
<![]() или
или ![]() >
>![]() . Если
. Если
![]() (при
(при ![]() >
>![]() ) для некоторого
) для некоторого ![]()
![]() ;
; ![]() >
>![]() , что противоречит предположению.
Аналогичным способом приводится к противоречию случай
, что противоречит предположению.
Аналогичным способом приводится к противоречию случай ![]() >
>![]() . Следовательно,
. Следовательно, ![]() и
и
![]() . Видно, что
. Видно, что ![]() .
Случай 2 доказан.
.
Случай 2 доказан.
Таким образом
доказано, что при любых значениях ![]() равенство
равенство ![]() не выполняется. Аналогичным образом это
относится к случаю, если
не выполняется. Аналогичным образом это
относится к случаю, если ![]() – простое число (
– простое число (![]() ). Это означает, что если
). Это означает, что если ![]() и
и ![]() простые
числа, которые являются сомножителями составного нечетного числа
простые
числа, которые являются сомножителями составного нечетного числа ![]() , то это число может также являться
произведением простого нечетного числа
, то это число может также являться
произведением простого нечетного числа ![]() на
на ![]() >1. В случае, если бы
>1. В случае, если бы ![]() являлось простым числом, то аналогично
(как и в том случае, если бы
являлось простым числом, то аналогично
(как и в том случае, если бы ![]() было составным
числом) имеем
было составным
числом) имеем ![]() .
.
Следовательно,
если ![]() – иррегулярное простое число, т. е.
– иррегулярное простое число, т. е. ![]() , разделим один из сомножителей на
, разделим один из сомножителей на ![]() , а другой умножим на
, а другой умножим на ![]() , где
, где ![]() выбрано
таким образом, что
выбрано
таким образом, что ![]() >
>![]() ;
; ![]() >1 (
>1 (![]() ) (
) (![]() ). Тогда
). Тогда
![]() .
.
Таким
образом, ![]() – регулярное простое число.
– регулярное простое число.
В случае,
если ![]() , имеем:
, имеем:
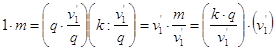 .
.
Для
обоснования общей закономерности делимости чисел, когда ![]() есть
целое или дробное число (после деления
есть
целое или дробное число (после деления ![]() на
на ![]() ) заметим, что любое натуральное число
) заметим, что любое натуральное число ![]() делится на
делится на ![]() (при
(при
![]() ) независимо от того является ли число
) независимо от того является ли число ![]() дробным или целым [6].
дробным или целым [6].
Что касается
простого целого иррегулярного числа ![]() , то это аналогично
(что число
, то это аналогично
(что число ![]() делится на
делится на ![]() ),
где
),
где ![]() – всегда дробное число
– всегда дробное число ![]() (при
(при ![]() ), где
), где
![]() - регулярное простое число.
- регулярное простое число.
Поэтому на
прямой линии (по масштабу) независимо от того является ли число ![]() целым
целым ![]() или
дробным
или
дробным ![]() , оно откладывается
, оно откладывается ![]() раз и в результате (по масштабу) на
прямой линии образуется целое число
раз и в результате (по масштабу) на
прямой линии образуется целое число ![]() .
.
В этом общее
сходство в закономерности делимости делящегося числа ![]() на
на
![]() и не делящегося, которым аналогично
обладает простое иррегулярное число
и не делящегося, которым аналогично
обладает простое иррегулярное число ![]() при делении его на регулярное
простое число
при делении его на регулярное
простое число ![]() , что представляет частный
случай деления числа
, что представляет частный
случай деления числа ![]() на
на ![]() ,
когда
,
когда ![]() не является целым числом.
не является целым числом.
Это значит,
что, если иррегулярное простое число ![]() не делится на
регулярное простое число
не делится на
регулярное простое число ![]() (
(![]() – дробное число
– дробное число ![]() ),
то имеет место сравнение
),
то имеет место сравнение ![]() , аналогично тому,
как
, аналогично тому,
как ![]() (где
(где ![]() – целое
число
– целое
число ![]() ), либо
), либо ![]() ,
если
,
если ![]() – дробное число, равное
– дробное число, равное ![]() (при
(при ![]() ). При
этом
). При
этом ![]() равноценно сравнению
равноценно сравнению
c. а≡0(mod c).
Известно [3-5],
что ![]() ; но
; но ![]() , где
, где
![]() , т. е. делится на
, т. е. делится на ![]() .
.
Допустим ![]() не делилось бы на
не делилось бы на ![]() , то и в этом случае
, то и в этом случае ![]() (h:h1=h2) Это
означает, что независимо от того делится или не делится
(h:h1=h2) Это
означает, что независимо от того делится или не делится ![]() на
на
![]() (является или не является
(является или не является ![]() произведением двух сомножителей числа
классов:
произведением двух сомножителей числа
классов: ![]() ,
, ![]() делилось
бы на дробное число >1, которое являлось бы нецелым.
делилось
бы на дробное число >1, которое являлось бы нецелым.
Аналогично,
если ![]() делится на
делится на ![]() , то
в случае, если
, то
в случае, если ![]() – иррегулярно, имеем
– иррегулярно, имеем ![]() (где
(где![]() –
целое число от деления числителя чисел Бернулли
–
целое число от деления числителя чисел Бернулли ![]() на
иррегулярное
на
иррегулярное ![]() ).
).
В случае,
если ![]() (где
(где ![]() –
дробное число >1 от деления числителя чисел Бернулли
–
дробное число >1 от деления числителя чисел Бернулли ![]() на
регулярное
на
регулярное ![]() , то в обоих случаях
, то в обоих случаях ![]() независимо от того
независимо от того ![]() делит
делит![]() или
или ![]() не делит
не делит ![]() ) [6].
) [6].
Из литературы
[3-5] известно, что ![]() тогда и только тогда делит
числитель числа
тогда и только тогда делит
числитель числа ![]() (в нашем случае оно обозначено
(в нашем случае оно обозначено
![]() ), когда
), когда ![]() ,
если
,
если ![]() не делит числители чисел Бернулли
не делит числители чисел Бернулли ![]() , то второй сомножитель
, то второй сомножитель ![]() в выражении
в выражении ![]() отличен
от нуля по модулю
отличен
от нуля по модулю ![]() (в нашем случае
(в нашем случае ![]() ) в
) в ![]() случаях
случаях![]() , т. е.
, т. е. ![]() , но
, но![]() , где
, где ![]() дробное
или целое число
дробное
или целое число ![]() не зависимо от того
не зависимо от того ![]() или несравнимо.
или несравнимо.
Как известно
[5], ![]() – число классов эквивалентности
дивизоров. Предел
– число классов эквивалентности
дивизоров. Предел ![]() одинаков при суммировании по
любому классу. Поэтому
одинаков при суммировании по
любому классу. Поэтому ![]() , где суммирование
происходит по всем классам, и равен числу
, где суммирование
происходит по всем классам, и равен числу ![]() ,
умноженному на предел
,
умноженному на предел ![]() , где суммирование распространено
на главный класс.
, где суммирование распространено
на главный класс.![]()
![]() ;
; ![]()
![]() – индекс группы единиц вида:
– индекс группы единиц вида: ![]() в группе всех единиц. В связи с
изложенном выше теорема Ферма соответствует формулировке: «Доказать, что
уравнение xр + yр = zр не имеет решений в
целых числах при n≥3 не зависимо от того делит или не делит простой
показатель р числители чисел Бернулли». Теорема Ферма на основании вышеизложенного
доказана.
в группе всех единиц. В связи с
изложенном выше теорема Ферма соответствует формулировке: «Доказать, что
уравнение xр + yр = zр не имеет решений в
целых числах при n≥3 не зависимо от того делит или не делит простой
показатель р числители чисел Бернулли». Теорема Ферма на основании вышеизложенного
доказана.
На основе полученных результатов и имеющихся литературных источников предлагается следующее:
1. Доказать, что уравнение xn +yn+zm +sm=tp не имеет решений в целых числах , где x≠y≠z≠s≠t≠0, m,n,p-простые числа; n,m,p≥5; х,y,z,s,t-простые нечетные числа.
2. Доказать, является или не является число 1.2.3.5.7.11…m + 1..3.5.7.11…n степенью целого числа (то есть 1.2.3.5.7.11…m + 1..3.5.7.11…n=zp), где m≠n≠p≠0, m,n,p – простые числа x≠y≠0.
3. Доказать, что любое простое нечетное число m можно представить в виде 2n + k=m, где n≥1, k-простое нечетное число.
Литература
1. Серпинский В. Что мы знаем и чего не знаем о простых числах. М.: Издательство иностранной литературы. Пер. с польского.-1963.- 89 с.
2. Воронин С.М. Простые числа. М.: Знание.-1978.-63 с.
3. Боревич З.И., Шафаревич Н.Р. Теория чисел. М.: Наука.–1985.– 368 с.
4. Постников М.М. Введение в теорию алгебраических чисел. М.: – 1980. –Наука– 239 с.
5. Эдвардс Г. Последняя теорема Ферма. М.: Мир.–1980.– 480 с.
6. Карпунин И.И., Подлозный Э.Д. К вопросу о делимости чисел / Сучаснi проблеми науки та освiти. 8-а Мiжнародна мiждисциплiнарна науково-практична школа-конференцiя. Харькiв – 2007. – С. 80.
Поступила в редакцию 29.05.2014 г.