Оптимальное управление в задаче химической кинетики

 

Дикусар Василий Васильевич,

доктор физико-математических наук, профессор, главный научный сотрудник Вычислительного центра им. Дородницына РАН,

Вуйтович Марек,

кандидат физико-математических наук, доцент кафедры информатики и математики Технолого-гуманитарного университета им. Казимира Пулаского в Радоме,

Султанов Василь Ризифович,

аспирант Вычислительного центра им. Дородницына РАН,

Нуждин Дмитрий Олегович,

аспирант Московского физико-технического института (государственного университета).

 

Постановки задач

 

Фьюмингование шлаков предназначено для извлечения из них полезных металлов (олово, свинец, цинк и др.). Наиболее распространённый процесс связан с продувкой через расплавленный шлак, содержащий окислы извлекаемых металлов, смеси тонкодисперсного пылеугля с воздухом. Часть угля сгорает в шлаковой ванне и за счёт выделившегося тепла поддерживает шлак в жидком состоянии. Другая часть введённого в ванну углерода является восстановителем и при соприкосновении со шлаком восстанавливает извлекаемый металл, который переходит в газообразную форму в виде паров и уносится из ванны вместе с отходящими газами. В дальнейшем пары металла (в основном цинка) окисляются воздухом и превращаются в пыль, которая улавливается в специальных фильтрах, а затем извлекается. Металлический цинк получается путём химической обработки пылевидного содержимого фильтра.

Периодический процесс фьюмингования начинается с заливки в печь определённого количества расплавленного шлака. Затем начинается продувка шлака углевоздушной смесью и в результате возгонки цинка содержание последнего в шлаке с течением времени снижается. Процесс заканчивается, когда остаточное содержание цинка в шлаке снижается до 1-2%, после чего дутьё прекращается, шлак сливается, а на его место заливается новая порция шлака. Оптимальное ведение процесса имеет целью сократить время извлечения из шлака содержащегося в нём цинка. Сокращение времени цикла влияет на экономику в 2-х направлениях: во-первых, увеличивает производительность агрегата, а во-вторых сокращает расход дорогостоящей угольной пыли. Ход процесса приближённо описывается системой нелинейных обыкновенных дифференциальных уравнений.

 

Задача А₁

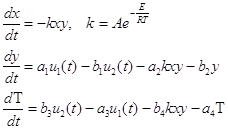                                                                                 (1)

 

 

 

                                                         (2)

 

Здесь – массовая концентрация окиси цинка в шлаке;  – концентрация восстановителя в зоне реакции; – температура в шлаковой ванне; – макроскопическая константа скорости реакции;  (управление) – скорость потока угольной пыли, поступающей с дутьём в аппарат;  (управление) – скорость расхода воздуха.

Остальные переменные представляют собой константы.

Начальные условия:

.                                                                (3)

Краевые условия:

 – свободны.                                                            (4)

Требуется определить  при условиях (1) – (4).

Решение задачи А₁ наталкивается на ряд принципиальных затруднений которые связаны с варьированием времени процесса . В целях облегчения получения решения перейдём к следующей задаче.

 

Задача А₂

Определить  при наличии ограничений (1) – (3) и краевых условиях  – свободны                                                                                              (5)

 

Теорема 1

Задачи А₁ и А₂ эквивалентны.

Доказательство следует из монотонного убывания функции . Монотонность следует из системы (1) при условиях: .

Необходимое условие экстремума

Составим функцию Понтрягина:

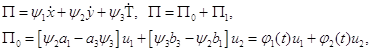                         (6)

 

где  и  носят название функции переключения.

Сопряжённые функции удовлетворяют следующей системе дифференциальных уравнений:

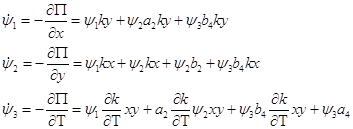                             (7)

 

 

 

Граничные условия системы (7) имеют вид:

                                                             (8)

Оптимальное управление выбирается из условия  если  и  если ,  если и  если .

Таким образом решение исходной задачи А₂ редуцируется к краевой задаче для сопряжённой системы уравнений (7) при краевых условиях (8). В результате получаем двухточечную трёхпараметрическую краевую задачу по выбору начальных значений  таким образом, чтобы удовлетворить краевым условиям (8).

При наличии фазового ограничения  система сопряжённых уравнений заменяется на систему

,                                                           (9)

.

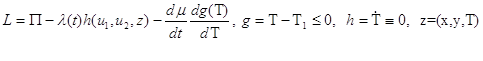здесь - обобщенная функция.

 

Условие дополняющей нежёсткости примут вид:

Рассмотрим теперь возможность существования особых режимов в задаче А₂. Сперва рассмотрим случай  на некотором интервале. Здесь при такой ситуации принцип максимума не позволяет определить управление .

Выпишем теперь более подробно условие существования особых режимов.

, ,                                        (10)

Соотношения (10) в силу основных и сопряжённых систем уравнений определяют выбор управления  при особом режиме.

Аналогичным образом определяются особые режимы в случае . При этом не исключается случай одновременного выполнения условий  и . , ,

Перейдём теперь к вопросам существования решений в задаче А₂.

 

Теорема 2.

Оптимальное управление в задаче А₂ существует.

Доказательство.

В силу ограничений (2) для правой части уравнений (1) выполнено условие Филиппова. Из условий (2) также следует существование допустимого управления  и . Оптимальное управление существует.

 

Теорема 3 (теорема единственности)

Оптимальное управление в задаче А₂ единственно.

Доказательство.

Из граничных условий для сопряжённых переменных (8) следует, что  где С – константа.

Из основной системы дифференциальных уравнений (1) следует, что

.

Отсюда получаем единственность решения.

 

Задача А₃

Дифференциальные уравнения: , , , 0≤t≤t₁. u₁₁≤u₁(t)≤u₁₂, u₂₁≤u₂(t)≤u₂₂, T(t)≤T₁. , x(0)=90, y(0)=3, T(0)=70, y(t₁), z(t₁) – свободны, T₁=90, t₁=110, u₁₁=0, u₂₁=0, u₁₂=40, u₂₂=85. Функционал x(t₁)→min.

 

Данная задача имеет решение вида:

x(t)=90exp[-0.026t], y(t)=exp[0.023t]+2,

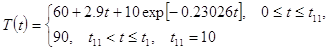 u₁(t)=40,

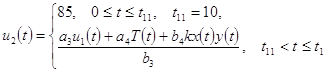, a₃=2, b₃=1, a₄=0.02, b₄=1, k=0.0141755,

 

которое получается при выборе управлений u₁(t)=u₁₂, u₂(t)=u₂₂ при 0≤t≤t₁₁, причем момент времени t₁₁ определяется достижением переменной T(t) своего фазового ограничения: T(t₁₁)=T₁. При t₁₁<t≤t₁ управление u₁(t) остается на верхней границе u₁(t)=u₁₂, а управление u₂(t) выбирается из условия T(t)=T₁, или .

Данное решение представлено на графике (рис. 1). Величина функционала в этом случае равна x(t₁)=5.1542.

 

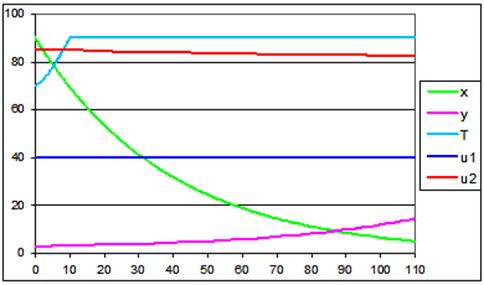
Рис. 1.

 

Литература

 

1.                  Афанасьев А.П., Дикусар В.В., Милютин А.А., Чуканов С.В. Необходимое условие принципа максимума. М., Наука, 1990.

2.                  Федоренко Р.П. Приближенное решение задач оптимального управления. М., Наука, 1978.

3.                  Шалашилин В.И.. Кузнецов Е.Б. Метод продолжения решения по параметру и наилучшая параметризация, М.: УРСС. 1999.

4.                  Фигура А., Методы продолжения решений в прикладных задачах оптимального управления, Автореферат диссертация д.ф.-м.н. ИПУ РАН 2001.

5.                  Дикусар В.В., Оленёв Н.Н. Минимизация конвективного и радиационного теплового потока при входе аппарата в атмосферу // Высокопроизводительные параллельные вычисления на кластерных системах. Материалы XIII Всероссийской конференции (Н. Новгород, 14–16 ноября 2013 г.) / Под ред. проф. В.П. Гергеля. – Нижний Новгород: Изд-во Нижегородского госуниверситета, 2013. С.108-113.

 

Поступила в редакцию 11.08.2014 г.