Эффект Арнольда – Филатова. Золотое, серебряное сечения. Альтернативная запись бесконечно сложной последовательности. Аргументация по фундаментальности «Потоковой теории»
Филатов Олег Владимирович,
инженер-программист НТЦ Модуль,
Филатов Илья Олегович,
ученик 9 класса школы № 1468, г. Москва.
Академик РАН, математик, Владимир Игоревич Арнольд ввёл понятие бинарной сложности (для: слов, спектров, цуг, составных событий). Экспериментально бинарная сложность, была обнаружена О.В. Филатовым в потоковой последовательности, имитирующей выпадение монеты. Обнаруженное преобладание составных событий низкой бинарной сложности над составными событиями с высокой бинарной сложностью получило название «Эффект Арнольда – Филатова».
Ключевые слова: бинарная сложность, потоковая последовательность, случайная бинарная последовательность, максимально сложная последовательность, составное событие, выпадение монеты, цуга, спектр, золотое сечение, серебряное сечение, академик Владимир Игоревич Арнольд, эффект Арнольда – Филатова.
Сокращения: пос-ть – последовательность, ф. – формула.
Выпадение составных событий разных длин после мишени
В работах [1, 2] рассматривался результат подбрасывания монеты в виде бинарной пос-ти: «10100110011100010000111101011101100110101…». В таких пос-ях есть участки с повторяющимися составными событиями (подчёркнуты «001100»). В работах [1, 2] даны формулы, по которым можно рассчитать, сколько выпадет таких участков при N подбрасываниях монеты. Эти формулы начинают работать тогда, когда комбинаторные формулы с факториалами перестают работать из-за того, что вычисления факториалов приводят к слишком большим числам, которые вычислительные средства не поддерживают. Формулы, из работ [1, 2], на тех же самых вычислительных средствах рассчитывают «сгустки» выпадений монеты для тысяч, миллионов, миллиардов и т.д. подбрасываний монеты. Более того, любую последовательность выпадений монеты стало возможно раскладывать на рассчитываемые по формулам спектры - цуги. Стала возможна констатация факта, что любая выпавшая последовательность из результатов подбрасываний монеты является суммой спектров (цуг), работы [1, 2, 3].
Математическое ожидание выпадающих за мишенью событий длины n
Пусть в
потоковой пос-ти после завершения выпадения составного события ![]() длиной m ищется
длина n составного события
длиной m ищется
длина n составного события ![]() , выпадающего за
, выпадающего за ![]() . Пример: «…1110?», «…0001?»
- завершение некоего составного события
. Пример: «…1110?», «…0001?»
- завершение некоего составного события ![]() обозначает
подчёркнутый перепад (инверсия). Вопросительные знаки символизируют не определённость
длины выпадающего за
обозначает
подчёркнутый перепад (инверсия). Вопросительные знаки символизируют не определённость
длины выпадающего за ![]() события
события ![]() . Так как длина
. Так как длина ![]() обратно
пропорциональна 2n (вероятность выпадений заданных сторон монеты),
то формула расчёта математического ожидания выпадающих за мишенью событий
обратно
пропорциональна 2n (вероятность выпадений заданных сторон монеты),
то формула расчёта математического ожидания выпадающих за мишенью событий ![]() длины n, будет:
длины n, будет:
![]() (0)
(0)
Пример. Есть тысяча составных
событий моды три ![]() . По (0) рассчитать математические ожидания
выпадающих за
. По (0) рассчитать математические ожидания
выпадающих за ![]() следующих составных событий:
следующих составных событий:
![]() ;
; ![]() ;
; ![]() . После тысячи
событий
. После тысячи
событий ![]() выпадет: 500
событий
выпадет: 500
событий ![]() первой моды; 125
событий
первой моды; 125
событий ![]() третьей моды; два
события
третьей моды; два
события ![]() девятой моды.
девятой моды.
Бинарная сложность
По академику Арнольду разные цуги (спектры) одинаковой длины могут обладать разной сложностью [7]. И результат выпадения монеты «101», является более сложным, чем «111».
По академику Арнольду сложность – это число возможных трансформаций. В таблице 1 расписана сложность уровней монады (название ак. Арнольда) для четырёх цуг (слов) n=1Сw=3 : «010», «101», и n=3Сw=1: «111», «000» (о цугах [1, 2, 3]).
Таблица 1.
|
Уровень сложности |
1С3 = «010» |
1С3 = «101» |
3С1= «111» |
3С1 = «000» |
|
1 |
110 |
110 |
111 |
000 |
|
2 |
011 |
011 |
|
|
|
3 |
101 |
101 |
|
|
|
исходное состояние |
110 |
110 |
|
|
Из таблицы 1 видно, что сложность цуг 1С3 («010», «101») равна между собой и выше чем сложность цуг 3С1 («000», «111»). Так как число возможных преобразований по академику Арнольду для 1С3 равно трём (четыре возможных состояния, два из которых тождественны). А число возможных преобразований для 3С1 равно нулю (спектр не изменяется).
Действительно, в потоковых последовательностях имитирующих большое число подбрасываний монеты [1, 2, 3], численно преобладают простые (последовательные) цуги («000», «111», …) над сложными (инверсными) цугами («010», «101», …). Разница между бинарными пос-тями с их уникальными свойствами и другими типами пос-тей, получаемых при подбрасывании монеты описана в [5]. Забегая вперёд, отмечу, что эксперименты в работах [1, 2, 3], и (1.1) показывают четырёхкратное преобладание простых (последовательных) составных событий над сложными (инверсными) событиями (цугами, словами) той же длины.
Число цуг ![]() в потоковой пос-ти
F(N) рассчитывается по (1) [2, 3]:
в потоковой пос-ти
F(N) рассчитывается по (1) [2, 3]:
![]() (1)
(1)
где: N – число бросков монеты (N ≥ 103), n – базовая длина составного события в цуге [1, 2], w – число полуволн в цуге [3].
Большое число опытов по подбрасыванию монеты короткими сериями, с последующей сортировкой результатов, свидетельствуют о равных вероятностях выпадений комбинаций равной длины. Например, таких, как в таблице 1. Но при переходе к потоковой пос-ти подбрасываний монеты, отношение числа найденных в ней цуг 3С1 («111») однозначно больше, чем цуг 1С3 («010»). Казалось бы, цуги одинаковой длины («111», «010») должны встречаться одинаковое число раз (с точностью до случайной флуктуации). Но для цуг одинаковой длины («111», «010») в потоковой пос-ти это не так. И эксперименты на физических монетах, и компьютерное моделирование подбрасывания монеты выдают существенно разные количества цуг («111», «010») не смотря на их равную длину. Глубинное научное объяснение этому факту дал академик Арнольд, введя понятие бинарной сложности [7].
Численные соотношения в цугах с разной бинарной сложностью
Пусть
выполняется условие n = w = x . В котором: n – базовая длина
составного события цуги, w - число полуволн цуги. Тогда цуга ![]() будет обладать меньшей бинарной
сложностью, как последовательное составное событие
будет обладать меньшей бинарной
сложностью, как последовательное составное событие ![]() , из выпавших x
раз подряд нулей или единиц (010203..0x).
А цуга
, из выпавших x
раз подряд нулей или единиц (010203..0x).
А цуга ![]() будет обладать большей бинарной
сложностью, по сравнению с
будет обладать большей бинарной
сложностью, по сравнению с ![]() . Так как цуга
. Так как цуга ![]() есть объединение следующих x раз
друг за другом инверсных событий, нулей и единиц (01120314..1x).
есть объединение следующих x раз
друг за другом инверсных событий, нулей и единиц (01120314..1x).
Отношение
численности событий ![]() в потоковой пос-ти к
в потоковой пос-ти к ![]() рассчитывается по ф.2.0. Оно не зависит
от числа N -бросков монеты.
рассчитывается по ф.2.0. Оно не зависит
от числа N -бросков монеты.
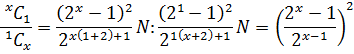
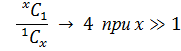 (2)
(2)
(2) можно переписать в виде неравенства:
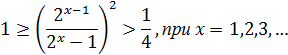 (2.1)
(2.1)
В более общем случае, когда n ≠ w, ф.2.0 можно переписать в виде ф.3. Отношение двух любых цуг n1Сw1 / n2Сw2 с любыми числами полуволн w1, w2 и числами длин n1, n2 не зависит от N - числа бросков монеты (эл).
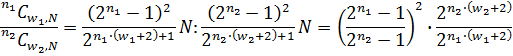 (3)
(3)
Таблица 2 рассчитана по (3). В таблице 2 приведены отношения цуг (слов) одинаковой длины (n1*w1 = n2*w2), но разной бинарной сложности.
Пример. На пересечение столбца 1 и строки 3 указаны две пары бинарных цуг: n1Сw1 =[«110011» = «001100»] ; (n1=2, w1=3) и n2Сw2 = [«101010» = «010101»]; (n2=1, w2=6). Длина обеих цуг n1Сw1 и n2Сw2 рана 6 элементарным событиям (элам): n1*w1= n2* w2=6. Казалось бы, количество любых слов одинаковой длины одинаково. Но в потоковой пос-ти это не так. По академику Арнольду спектры «110011» =«001100» обладает меньшей бинарной сложностью, так как в них меньше инверсий (две инверсии внутри спектра), по сравнению со спектрами «101010»= «010101» . В которых больше инверсий, пять инверсии внутри спектра – большая бинарная сложность. Отношение числа спектров «110011» и «001100» к числу спектров «101010» и «010101» в потоковой пос-ти будет равно 2,25 – ячейка 4 в столбце 1 таблицы 2.
Таблица 2.
«Отношение численностей цуг одинаковой длины, но разной бинарной сложности, отвечающих условию: n1*w1 = n2*w2».
|
|
1 |
2 |
3 |
|
1 |
(n1=2,w1=1) n1*w1 = 2 (n2=1,w2=2) n2*w2 = 2 |
(n1=3,w1=1) n1*w1 = 3 (n2=1,w2=3) n2*w2 = 3 |
(n1=4,w1=1) n1*w1 = 4 (n2=1,w2=4) n2*w2 = 4 |
|
2 |
(n1=2,w1=2) n1*w1 = 4 (n2=1,w2=4) n2*w2 = 4 |
(n1=3,w1=2) n1*w1 = 6 (n2=1,w2=6) n2*w2 = 6 |
(n1=4,w1=2) n1*w1 = 8 (n2=1,w2=8) n2*w2 = 8 |
|
3 |
(n1=2,w1=3) n1*w1 = 6 (n2=1,w2=6) n2*w2 = 6 |
(n1=3,w1=3) n1*w1 = 9 (n2=1,w2=9) n2*w2 = 9 |
(n1=4,w1=3) n1*w1 = 12 (n2=1,w2=12) n2*w2 = 12 |
|
4 |
n1Сw1 / n2Сw2 = 2,25 |
n1Сw1 / n2Сw2 = 3,0625 |
n1Сw1 / n2Сw2 = 3,515625 |
Строки 1, 2, 3 в таблице 2 содержат пары спектров разных длин. Но, не смотря на разные длины спектров в парах, отношения цуг в каждой паре оказывается одинаковым. Так в столбце 1, строка 1 вписана пара цуг n1=2Сw1=1 и n2=1Сw2=2 . Длина каждой цуги в элементарных событиях (элах) равна двум: n1*w1 = n2*w2 = 2. Их отношение друг к другу равно 2,25 – строка 4. Но такое же отношение будет и для спектров в строках 2 и 3. Хотя их длины в элементарных событиях (элах) будут 4 и 6.
Отсюда можно сделать вывод, что для спектров отвечающих условию: n1*w1 = n2*w2 – отношение n1Сw1 / n2Сw2 не зависит от их численности в потоковой пос-ти. А зависит от числа внутренних инверсий внутри спектра – сложности, по академику Арнольду.
Таблица 3 является продолжением таблицы 2 (рассчитанной по (3)), в которой убрана излишне подробная информация.
Таблица 3.
«Отношение численностей цуг одинаковой длины, но разной бинарной сложности, отвечающих условию: n1*w1 = n2*w2».
|
n1; w1 n2; w2 n1Сw1 / n2Сw2 |
5; 1 1; 5 3,7539 |
6; 1 1; 6 3,8759 |
7; 1 1; 7 3,937744 |
8; 1 1; 8 3,968811 |
9; 1 1; 9 3,98439 |
10; 1 1; 10 3,992191 |
21; 1 1; 21 3,999996 |
Экспериментально обнаруженные в потоковой пос-ти (эквивалентной 2*107 последовательным броскам монеты) цуги представлены в виде таблицы и графика на рис. 1. С помощью таблицы рис. 1 можно рассчитать часть отношений таблицы 2. И убедиться, что экспериментальные данные хорошо совпадают с формульными расчётами. Например, величина отношения, полученного в эксперименте цуг: 3С1 / 1С3 = 956375 / 312721 = 3,0582 хорошо совпадает с рассчитанной в таблице 2 по (3) величиной - 3,0625 (таб. 2, столбец 2, строка 4).
Чем выше бинарная сложность, тем меньше в потоковой последовательности событий обладающих ею.
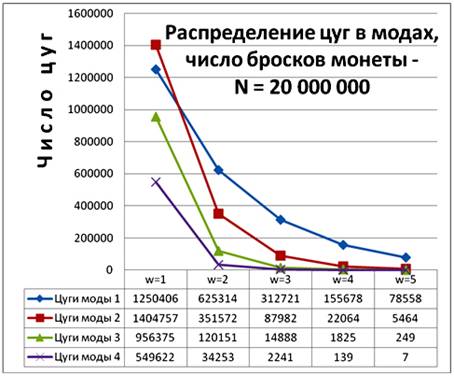
Рис. 1.
Потоковая (максимально сложная) бинарная последовательность – состоит из цуг
По Джозефу Форду случайная бинарная последовательность является максимально сложной. «Бесконечные максимально сложные пос-ти настолько непредсказуемы, что их нельзя вычислить с помощью какого-либо конечного алгоритма; задать такую последовательность можно, только предъявив её копию» [6].
Утверждение, что бесконечную случайную последовательность можно задать только с помощью её копии говорит о её не сжимаемости. Но, как видно из работ [1, 2, 3], любая бесконечная, максимально сложная пос-ть образуется цугами. Число цуг в ней - N/3, где N – число эл (подбрасываний монеты) пос-ти.
Любая цуга ![]() представима в
виде упорядоченной пары чисел: n, w. Где n – длина базовой полуволны
(составного события), а w – число полуволн в цуге. Разворачивание этой пары
чисел в бинарную пос-ть производится по алгоритму, и, следовательно, является
алгоритмом. Примеры разворачивания цуг (n=1Cw=3=«1S1S1S»=«101»,
n=2Cn=2 = «2S2S» = «1100») подробно
описаны в работе [2]. Таким образом, любую случайную пос-сть можно представить
из алгоритмов разворачивания цуг
представима в
виде упорядоченной пары чисел: n, w. Где n – длина базовой полуволны
(составного события), а w – число полуволн в цуге. Разворачивание этой пары
чисел в бинарную пос-ть производится по алгоритму, и, следовательно, является
алгоритмом. Примеры разворачивания цуг (n=1Cw=3=«1S1S1S»=«101»,
n=2Cn=2 = «2S2S» = «1100») подробно
описаны в работе [2]. Таким образом, любую случайную пос-сть можно представить
из алгоритмов разворачивания цуг ![]() . Число цуг
равно трети от числа случайных событий N составляющих пос-сть.
. Число цуг
равно трети от числа случайных событий N составляющих пос-сть.
Цуги - новый уровень структурной организации бинарной потоковой (максимально сложной) пос-ти. И, можно попробовать, сжать распределение цуг, а не бинарные элементарные события.
Запись цуг бинарной (максимально сложной) пос-ти через(n, w) пары
В [1, 2]
показано, что число цуговых «кирпичиков» из которых собрано тело пос-ти равно ![]() . Именно
. Именно ![]() нужно (n, w) пар, что бы описать ими N
выпадений монеты.
нужно (n, w) пар, что бы описать ими N
выпадений монеты.
Формула (3) зависит от n, w параметров. Но n, w параметры можно использовать не только в формулах, (n, w) парами можно записывать цуги, из которых складывается любая потоковая пос-ть.
Упорядоченная запись случайной бинарной пос-ти в виде множества (n, w) пар чисел обладает свойствами вектора. Между n, w числами существует асимметрия, и можно определить какие числа в парах являются n - числами, а какие w - числами.
Обычный компьютерный файл с записью случайных чисел можно читать в двух направлениях: от начала к концу и от конца к началу. И никакими методами анализируя бинарные числа нельзя определить, где первое случайное событие в записанной потоковой пос-ти, а где последние.
Но, если следовать правилу, что в цуговых (n, w) парах на первом месте пишется n, а за ним w, то сумма n - чисел, и сумма w – чисел, после их сравнения, укажут направление от первой (n, w) пары к последней.
В работе [2], формула 5: nm = 2(n+1) , связывала через математическое ожидание число бросков монеты nm, которые нужно в среднем совершить в последовательности из N случайных бинарных событий, что бы выпало одно событие состоящие из n выпадений подряд. Так, например, для выпадения в потоковой пос-ти одного составного события, состоящего из десяти выпавших подряд орлов или решек, в среднем, ожидается 2048 = 2(10+1) бросков монеты. Здесь ключевые слова «для выпадения в потоковой пос-ти» - которые перечёркивают область действия формулы 1/2n - для подбрасывания монеты. Одной стороной формула 1/2n всегда упирается в край, в начало пос-ти, в первый бросок («в печку»). Формулы потоковой пос-ти, в отличие от 1/2n в край не упираются.
Для выпадения в пос-ти одного составного события, состоящего из ста сторон монеты подряд, в среднем нужно совершить: 2,5*1030= 2(100+1) бросков монеты. Событием из ста выпадений подряд одной стороны монеты может быть как цепочка из орлов, так и цепочка из решек.
Обратная задача – это найти наибольшую ожидаемую длину n события, состоящего из последовательных выпадений одной стороны монеты, в пос-ти из N бросков монеты. Это нужно для оценки верхней величины числа n при записи потоковой пос-ти через n, w пары.
Очевидно, задача будет решаться по обратной для (5) в [2] формуле. Формула (4), выдаёт ожидаемую n - длину серии (число выпадений монеты одной стороной подряд), единожды выпадающую в N подбрасываниях монеты:
![]() (4)
(4)
Так, в N=106 подбрасываниях монеты ожидается одна цепочка, из log(106) -1= 19 (девятнадцати) выпадений монеты одной стороной подряд.
Интересно
сравнить для пос-ти F(N), которая описывается цуговыми ![]() парами чисел (n,w),
наибольшее ожидаемое число для n и наибольшее ожидаемое число для w. Наибольшее
для n рассчитывается по (4).
парами чисел (n,w),
наибольшее ожидаемое число для n и наибольшее ожидаемое число для w. Наибольшее
для n рассчитывается по (4).
Наибольшее ожидаемое число для w будет, по представленному распределению в работах [1, 2] , равно числу цуг первой моды (n=1). Поэтому, в формуле 23 из работы [3] заменяем n на единицу, и получаем:
![]() (5)
(5)
Решаем в (5.1) уравнение относительно w:
![]() (5.1)
(5.1)
Сравнивая числа n, w, найденные по (4) и (5.1), между собой, замечаем, что: n – w = 2 и n > w. Это означает, что при записи потоковой последовательности (n, w) парами для обозначения n событий придётся, в среднем, использовать на два числа больше, чем для обозначения w событий.
Пример. Пусть
есть N=2*107 бросков монеты. Надо узнать, каким наиболее вероятным
множеством (n, w) чисел можно записать эту несжимаемую пос-сть. Для этого рассчитываем
значение n по ф.4:
![]() . Округляем
результат до 24. Ответ: данную потоковую последовательность можно описать
парами чисел
(n, w) которые лежат в диапазоне от 1 до 24. То есть 1 ≤ n ≤ 24; 1
≤ w ≤ 24 - 2 = 22.
. Округляем
результат до 24. Ответ: данную потоковую последовательность можно описать
парами чисел
(n, w) которые лежат в диапазоне от 1 до 24. То есть 1 ≤ n ≤ 24; 1
≤ w ≤ 24 - 2 = 22.
Золотое и серебряное сечения в потоковой (максимально сложной) бинарной последовательности
Таблица 4.
|
C0[1] = 37,5 C0[2] = 28,125 C0[3] = 16,406 C0[4] = 8,7890 |
C0[5] = 4,541 C0[6] = 2,307 C0[7] = 1,162 C0[8] = 0,583 |
C0[9] = 0,2925 C0[10] = 0,146 C0[11] = 0,073 … |
|
Button268: "Все nC0 %" SumProc = 100 Цуг= 6666666 |
||
Золотое сечение обнаруживается в потоковой (максимально сложной) пос-ти. В ней нулевые цуги первой моды C0[1] (подчёркнуты в таблице 4) составляют 37,5% от суммы цуг всех мод (nM, где n ≥ 1). Нулевые цуги всех остальных мод в сумме составляют 100% – 37,5% = 62,5 % . Полученные процентные отношения 37,5% и 62,5% хорошо совпадают с аналогичными процентными отношениями золотого сечения.
То есть природа противопоставляет цуги первой моды, например «10101» (1С0=37,5%) всем остальным цугам, например «1111100001111».
В работах [1, 2] представлены гистограммы, на которых отображаются экспериментально обнаруженные в потоковой пос-ти численности цуг. Так, в экспериментальной пос-ти из N равному 20 миллионов подбрасываний монеты [1], стр.61, было обнаружено 6665836 различных цуг (теоретическое число цуг N/3=6666667 цуг). Из них первой моде принадлежит 2500689 цуг. Таким образом, процент цуг первой моды к общему количеству цуг пос-ти, найденный экспериментальным путём, равен: 2500689*100/6665836 = 37,52%. Полученный в результате эксперимента процент (37,52%.) близок к величине золотого сечения для меньшей половины - 38,2 %.
Серебряное сечение также обнаруживается в потоковой пос-ти. Серебряное сечение возникает в результате деления числа элементарных событий входящих в нечётные составные события на число элементарных событий входящих в чётные составные события [1, 2].
В работах [1, 2]
приведено разделение, группировка, элементарных событий (подбрасываний монеты)
по чётным составным событиям и нечётным составным событиям. Оказалось, что
числа элементарных событий (элов, подбрасываний монеты) различаются для чётной
и нечётной области. В нечётной области группируется больше половины, ![]() элов. В чётной области сосредоточено
меньше половины
элов. В чётной области сосредоточено
меньше половины ![]() элов. Где N – число эл (подбрасываний
монеты). Отношение числа элементарных событий в этих областях будет:
элов. Где N – число эл (подбрасываний
монеты). Отношение числа элементарных событий в этих областях будет: ![]() .
.
Полученная величина - 1,25 хорошо совпадает с величиной серебряного сечения – 56/44 = 1,2727…
Обнаружение золотого сечения (золотых пропорций) и серебряного сечения (серебряных пропорций) в цуговых пропорциях потоковой (максимально сложной) последовательности нужно расценивать как проявление фундаментальных математических законов. То есть, принципы образования составных событий из элементарных бинарных событий (элов, подбрасываний монеты), привели к открытию цуг (цуги – цепочки составных событий). А в цуговых отношениях проявились фундаментальные для математики сечения: золотое и серебряное. Что является указателем на математическую фундаментальность самой потоковой теории.
Золотое сечение в n, w парах
Перемножая ![]() - базовую длину цуги n-ой моды (
- базовую длину цуги n-ой моды (![]() ) на число цуг
) на число цуг ![]() в моде, получим
абстрактную величину, принадлежащую n-ой моде и зависящую от числа N - бросков
монеты.
Сумма абстрактных величин всех мод зависит только от числа N, и равна 7N/9:
в моде, получим
абстрактную величину, принадлежащую n-ой моде и зависящую от числа N - бросков
монеты.
Сумма абстрактных величин всех мод зависит только от числа N, и равна 7N/9:
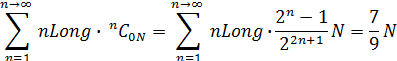 (6)
(6)
Отсюда, сумма ![]() - базовых длин
всех цуг
- базовых длин
всех цуг ![]() потоковой пос-ти F(N) равна 7N/9:
потоковой пос-ти F(N) равна 7N/9:
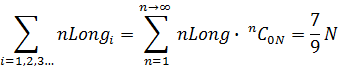 (6.1)
(6.1)
Тогда, ![]() - средняя базовая
длина, измеряемая
в элементарных событиях (элах), рассчитывается по (6.2):
- средняя базовая
длина, измеряемая
в элементарных событиях (элах), рассчитывается по (6.2):
![]() (6.2)
(6.2)
Теперь рассчитаем, по аналогии с (6), сумму всех w – являющихся вторыми числами в (n,w) парах и показывающих числа полуволн в цугах с длиной основания n. Сумма всех полуволн w является числом всех составных событий в потоковой пос-ти. В работах [1, 2] показано, что число составных событий потоковой пос-ти равно половине от числа бросков монеты:
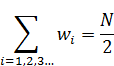 (7)
(7)
Количество чисел
которыми будет описаны все составные события пос-ти равняется N/3 - числу цуг в
потоковой пос-ти. Средняя величина такого числа ![]() рассчитывается в (7.1):
рассчитывается в (7.1):
![]() (7.1)
(7.1)
Процентная
величина: ![]() 60,9% примерно
равна большей половине золотого сечения (61,8 %). Процентная величина:
60,9% примерно
равна большей половине золотого сечения (61,8 %). Процентная величина: ![]() 39,1% близка по
величине меньшей половине золотого сечения (38,2 %).
39,1% близка по
величине меньшей половине золотого сечения (38,2 %).
Таким образом, близость производных продуктов из (n, w) пар к пропорциям золотого сечения, говорит о глубинном природном смысле их применения.
Дополнение к работе [5]
В работе [5] шла
речь о распределение всех составных событий ![]() первой моды (а
не только полярных) в n - разрядных бинарных словах. Числа
первой моды (а
не только полярных) в n - разрядных бинарных словах. Числа ![]() в таблице 6 рассчитываются по формуле (8):
в таблице 6 рассчитываются по формуле (8):
![]() (8)
(8)
Таблица 6.
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1Sn |
2 |
4 |
10 |
24 |
56 |
128 |
288 |
640 |
1408 |
|
|
2 |
6=2+4 |
16=2+6+10 |
40=2+6+10+24 |
96=40+56 |
224 |
512 |
1152 |
2560 |
Соседние члены ряда 1Sn, в таблице 6, связаны между собой по (8.1):
![]() (8.1)
(8.1)
Сумма членов
ряда ![]() , рассчитываемых по ф.8, с первого (n=1)
по n-й член включительно, находится по (8.2):
, рассчитываемых по ф.8, с первого (n=1)
по n-й член включительно, находится по (8.2):
![]() (8.2)
(8.2)
Резюме
Формулы «Потоковой теории» ранее не были открыты по двум причинам.
Первая причина – нужна доступная и мощная домашняя компьютерная техника, которая заменяет процесс подбрасывания монеты.
Вторая причина – нужно было ввести логическую условность, составное событие - nS (о составных событиях подробно написано в работах [1, 2]). Объявить, что события из нулей и единиц одинаковой длины (например: «000» = «111») являются одним и тем же, не различимым, составным событием одинаковой бинарной сложности. После введения этого логического обобщения количество рассматриваемых вариантов выпадений монеты резко сократилось. И сложность формул описывающих выпадение монеты уменьшилась.
Формулы «Потоковой теории» являются дополнением к известным комбинаторным и вероятностным формулам. Они начинают работать там, где завершают свою работу традиционные комбинаторные (факториальные) формулы и формула выпадения монеты – 1/2n. Если сравнить области работ для выше упомянутых формул в виде пространственных удалений от Земли, то традиционные формулы обслуживают области атмосферы и околоземного пространства, а формулы «Потоковой теории» обслуживают область всей оставшейся Вселенной.
Потоковая теория является фундаментальной теорией, так как описываемые ею распределения являются числами треугольника Паскаля [5]. Составляющие потоковой последовательности имеют пропорции Золотого и Серебряного сечений (эта статья).
В работе [4] открыт алгоритм, позволяющий получать в процессе подбрасывания монеты нужные пропорции составных событий при её выпадении, что является сенсационным фактом.
В этой работе описан «Эффект Арнольда – Филатова». Заключающийся в численном неравенстве цуг одинаковой длины, но с разной бинарной сложностью, в бинарной потоковой пос-ти. Формулы: 2.0; 2.1; 3 – описывают этот эффект.
Литература
1. Филатов О. В., Филатов И.О., Макеева Л.Л. и др. «Потоковая теория: из сайта в книгу». М.: Век информации, 2014. С.200.
2. Филатов О. В., Филатов И.О., Статья «О закономерностях структуры бинарной последовательности», «Журнал научных публикаций аспирантов и докторантов», № 5, 2014.
3. Филатов О. В., Филатов И.О., Статья «О закономерностях структуры бинарной последовательности (продолжение)», «Журнал научных публикаций аспирантов и докторантов», № 6, 2014.
4. Филатов О. В., Филатов И.О., Статья «О закономерностях структуры бинарной последовательности (продолжение 2)», «Журнал научных публикаций аспирантов и докторантов», № 7, 2014.
5. Филатов О. В., Статья «Бинарная потоковая последовательность – не Марковский процесс выпадения монеты. Бинарные слова и треугольник Паскаля», № 11, 2014.
6. Joseph Ford. «How random is a coin toss?» — Physics Today, April 1983, p. 40–47.
7. Владимир Игоревич Арнольд, Математический институт им. В. А. Стеклова, Москва. Публичная лекция 13 мая 2006 г. для школьников и студентов.
Поступила в редакцию 10.12.2014 г.