Создание программного обеспечения для решения кубических уравнений с использованием формулы Кардано
Симаков Егор Евгеньевич,
аспирант кафедры теории и методики обучения и воспитания Сахалинского государственного университета,
Захарова Лидия Владимировна,
ученица 10В класса информационно-технологического профиля МБОУ Лицей №1 г. Южно-Сахалинска.
Статья посвящена изучению методов решения кубических уравнений. Особое внимание уделяется формуле Кардано. В статье приведен подробный алгоритм решения уравнений третьей степени с использованием данного метода, а также его реализация в объектно-ориентированной среде Delphi.
Ключевые слова: формула Кардано, программирование, кубические уравнения.
Введение
Уже в древности люди осознали, как важно научиться решать алгебраические
уравнения вида ![]() – ведь к ним сводятся очень многие вопросы естествознания. Также проводились исследования по получению формул
для решения уравнений любой степени n, при помощи которых можно выразить
корни уравнения через его коэффициенты, т.е., решить уравнение в радикалах.
Однако только в XVI веке итальянским математикам удалось сформулировать
алгоритм решения уравнений третьей и четвертой степеней.
– ведь к ним сводятся очень многие вопросы естествознания. Также проводились исследования по получению формул
для решения уравнений любой степени n, при помощи которых можно выразить
корни уравнения через его коэффициенты, т.е., решить уравнение в радикалах.
Однако только в XVI веке итальянским математикам удалось сформулировать
алгоритм решения уравнений третьей и четвертой степеней.
Целью исследования является изучение существующих методов, а также разработка алгоритма и создание на его основе программного обеспечения для решения кубических уравнений на основе формулы Кардано.
Задачи исследования:
1. Рассмотреть различные методы решения уравнений третьей степени.
2. Изучить особенности применения формулы Кардано для решения кубических уравнений.
3. Создать программное обеспечение для решения кубических уравнений.
Методы решения кубических уравнений
В области комплексных чисел, согласно
основной теореме алгебры, кубическое уравнение всегда имеет 3 корня (с учётом
кратности). Так как каждый вещественный многочлен нечётной степени имеет хотя
бы один вещественный корень, все возможные случаи состава корней кубического
уравнения исчерпывается тремя, которые легко различаются с помощью дискриминанта
![]() [2]:
[2]:
· Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
· Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.
· Если Δ = 0, тогда хотя бы два корня совпадают. Это может быть, когда уравнение имеет двойной вещественный корень и ещё один отличный от них вещественный корень; либо, все три корня совпадают, образуя корень кратности 3.
Корни кубического уравнения ![]() связаны с коэффициентами
связаны с коэффициентами ![]() следующим образом:
следующим образом:
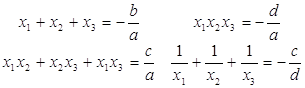
Исходя из основных свойств решения кубических уравнений,
необходимо дать определение понятию «комплексное число». Комплексные числа — числа вида x + y, где x и y –
вещественные числа, i – мнимая
единица, то есть: i2 = –1. Числа
x = Â(z) (или
Re z) и y =
Á(z) (или
Im z) называются соответственно вещественной
и мнимой частями z. Множество всех комплексных чисел обозначается ![]() . Если
комплексное число z = x + iy, то число
. Если
комплексное число z = x + iy, то число ![]() называется сопряжённым к z. [1]
называется сопряжённым к z. [1]
Наиболее распространенный метод решения кубических уравнений – метод перебора. [2] Сначала путём перебора находится один из корней уравнения (например, x1). Вторая стадия решения – это деление многочлена ax3 + bx2 + cx +d на двучлен x – x1 и решение полученного квадратного уравнения.
Алгоритм решения кубических уравнений с использованием формулы Кардано
В данном разделе статьи приведен подробный алгоритм решения уравнений третьей степени с помощи формулы Кардано. Данный алгоритм состоит из двух этапов. На первом этапе кубические уравнения приводятся к форме, в которой отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями. На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям. [3]
Рассмотрим алгоритм нахождения всех
корней кубического уравнения ![]() на основе
описанной выше формулы, а также ее тригонометрической интерпретации. [3,4] Приведем исходное
уравнение к каноническому виду. Для этого сделаем замену переменного по формуле
на основе
описанной выше формулы, а также ее тригонометрической интерпретации. [3,4] Приведем исходное
уравнение к каноническому виду. Для этого сделаем замену переменного по формуле ![]() :
: ![]() .
Раскрыв скобки в левой части уравнения, получим:
.
Раскрыв скобки в левой части уравнения, получим: ![]() .
Уравнение приведено к каноническому виду:
.
Уравнение приведено к каноническому виду:
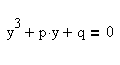
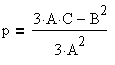
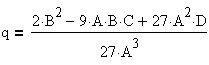
Дискриминантом уравнения ![]() называется число
называется число ![]() . Найдем решение полученного уравнения в
виде:
. Найдем решение полученного уравнения в
виде:
![]()
![]()
![]()
Число ![]() удовлетворяет
этому равенству, если числа m и n удовлетворяют системе из двух уравнений:
удовлетворяет
этому равенству, если числа m и n удовлетворяют системе из двух уравнений:
![]()
![]()
Находим числа m и n: ![]()
Дальнейшее решение зависит от знака дискриминанта S.
1. Пусть дискриминант меньше нуля. Тогда уравнение имеет три различных корня.
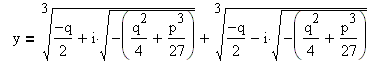
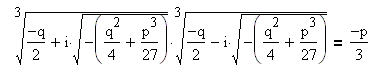
Найдём модуль комплексных чисел 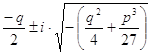 :
:
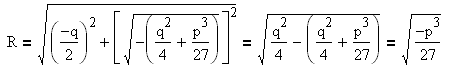
Аргумент числа 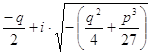 равен (в зависимости от знака q):
равен (в зависимости от знака q):
·
Если
![]() , то
, то 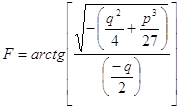
·
Если
![]() , то
, то 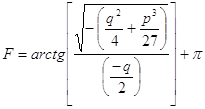
·
Если
![]() , то
, то ![]()
Для k=0, k=1, k=2 получаем решение:
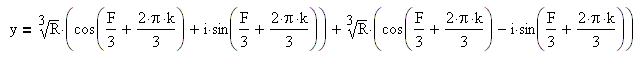
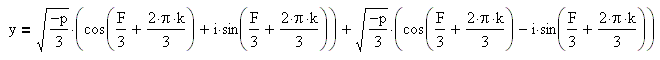
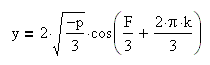
Итак, если дискриминант меньше нуля, то уравнение имеет три различных действительных корня:
![]()
2.
Пусть
дискриминант больше нуля. Тогда уравнение имеет один действительный
корень и два комплексно-сопряжённых.
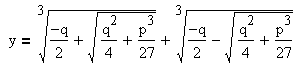
При этом для любых комплексных значений
корней необходимо выполнение условия: 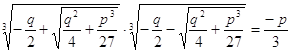 .
.
Примем аргумент F действительных
чисел, стоящих под знаком кубического корня, равным нулю. При этом модули этих
чисел могут принимать отрицательное значение. Аргумент кубического корня будет
принимать 3 значения: 0, 2*π/3, 4*π/3. Каждое решение y=y1,
y=y2, y=y3 будет состоять из суммы двух комплексных
чисел ![]() .
.
Число z1 находится в группе из трёх чисел:
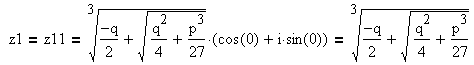
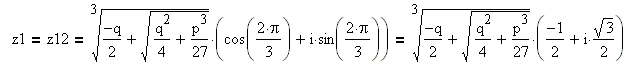
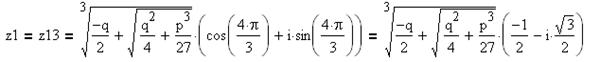
Число z2 находится в группе из трёх чисел:
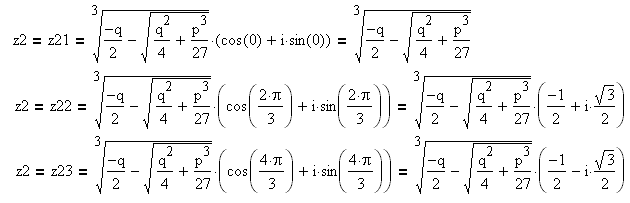
Для действительных значений кубических
корней выполняется обозначенное выше условие. Поэтому действительный корень
уравнения ![]() . Учитывая равенство
. Учитывая равенство 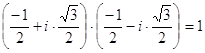 , получим два комплексно сопряжённых
корня:
, получим два комплексно сопряжённых
корня: ![]() ,
, ![]() .
.
Итак, если дискриминант больше нуля, то уравнение имеет один действительный корень и два комплексно-сопряжённых корня:
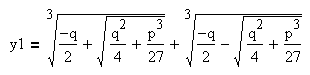
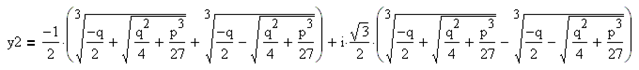
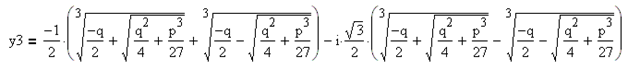
3.
Дискриминант
равен нулю. В
этом случае уравнение имеет три действительных корня, и два корня из трёх
обязательно совпадают друг с другом. Рассуждая точно так же, как в случае с
положительным дискриминантом, учитывая равенство ![]() ,
из формул корней уравнения с положительным дискриминантом получим:
,
из формул корней уравнения с положительным дискриминантом получим:
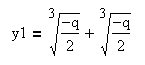
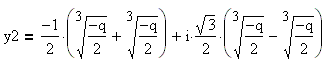
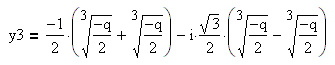
Итак, если дискриминант равен нулю, то
уравнение имеет три действительных корня, и два корня из трёх обязательно
совпадают друг с другом: ![]() .
.
Теперь получим решение исходного кубического
уравнения ![]() . Дискриминант этого уравнения
равен:
. Дискриминант этого уравнения
равен:
![]()
В зависимости от знака дискриминанта S возможны три случая:
·
Если
![]() , то:
, то:
![]()
·
Если
![]() , то:
, то:
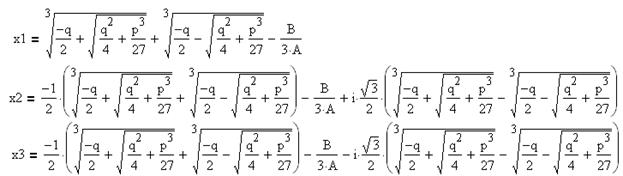
·
Если
![]() , то:
, то:
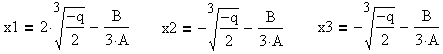
При этом: ![]() . Аргумент F вычисляется
по формулам, рассмотренным выше, исходя из знака q.
. Аргумент F вычисляется
по формулам, рассмотренным выше, исходя из знака q.
Реализация алгоритма в объектно-ориентированной среде программирования Delphi
Авторами статьи была создана программа в среде Delphi для решения кубических уравнений с использованием формулы Кардано по разработанному алгоритму, описанному выше.
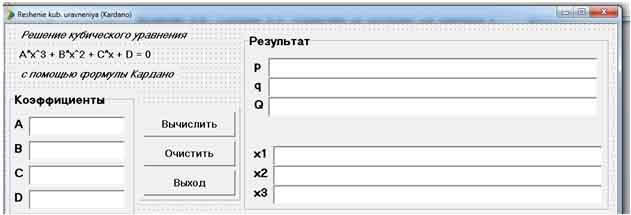
Рис. 1. Интерфейс программы для решения кубических уравнений.
Для решения уравнения пользователю необходимо ввести коэффициенты уравнения. Результат работы программы – коэффициенты уравнения в канонической форме (p и q), дискриминант (Q) и корни уравнения. Для создания интерфейса использовались следующие компоненты среды Delphi [5]:
· Label – для информирования пользователя о назначении программы, обозначения предназначения полей ввода – вывода;
· Button – для реализации основных действий программы (решения уравнения, очистки полей ввода-вывода, закрытия программы);
· Edit – для организации ввода-вывода данных;
· Panel и GroupBox – для группировки элементов на форме программы.
Рассмотрим код основных процедур программы.
Для решения уравнения необходимо объявить следующие переменные:
· A,B,C,D – коэффициенты исходного уравнения;
· p,q – коэффициенты преобразованного уравнения;
· QQ – дискриминант;
· F – аргумент комплексного корня;
· Re, Im – действительная и мнимая части комплексного корня;
· x1,x2,x3,y1,y2 – корни уравнения.
В программе предусмотрен контроль корректности ввода данных:
if (edit1.Text='') or (edit2.Text='') or (edit3.Text='') or (edit4.Text='') then
begin
Showmessage('Введите все коэффициенты уравнения');
Clear_Koeffs; Clear_Results;
end else begin
A:=strtofloat(edit1.Text); B:=strtofloat(edit2.Text);
C:=strtofloat(edit3.Text); D:=strtofloat(edit4.Text);
Процедуры Clear_Koeffs и Clear_Results осуществляют очистку полей ввода-вывода.
Процедура вычисления коэффициентов и дискриминанта преобразованного уравнения имеет следующий вид:
p := (3*A*C-power(B,2))/(3*power(A,2));
q := (2*power(B,3)-9*A*B*C+27*power(A,2)*D)/(27*power(A,3));
QQ := (4*power(3*A*C-power(B,2),3)+(power(2*power(B,3)
-9*A*B*C+27*power(A,2)*D,2)))/(2916*power(A,6));
edit5.Text := FloatToStr(p); edit6.Text := FloatToStr(q);
edit7.Text := floatToStr(QQ);
Вычисление корней уравнения происходит в зависимости от знака дискриминанта:
· Если дискриминант меньше нуля:
y1:=0; y2:=0; F:=0;
if QQ<0 then begin
if q<0 then F:=Arctan(-2*Sqrt(-QQ)/q);
if q>0 then F:=Arctan(-2*Sqrt(-QQ)/q)+Pi;
if q=0 then F:=Pi/2;
x1:=2*Sqrt(-p/3)*Cos(F/3)-B/A/3;
x2:=2*Sqrt(-p/3)*Cos((F+2*Pi)/3)-B/A/3;
x3:=2*Sqrt(-p/3)*Cos((F+4*Pi)/3)-B/A/3;
if q=0 then x3:=-B/A/3;
Edit8.Text := FloatToStr(x1); Edit9.Text := FloatToStr(x2);
Edit10.Text:= FloatToStr(x3);
end;
· Если дискриминант больше нуля:
if QQ>0 then begin
if -q/2+Sqrt(QQ)>0 then y1:=exp(ln(abs(-q/2+Sqrt(QQ)))/3);
if -q/2+Sqrt(QQ)<0 then y1:=-exp(ln(abs(-q/2+Sqrt(QQ)))/3);
if -q/2+Sqrt(QQ)=0 then y1:=0;
if -q/2-Sqrt(QQ)>0 then y2:=exp(ln(abs(-q/2-Sqrt(QQ)))/3);
if -q/2-Sqrt(QQ)<0 then y2:=-exp(ln(abs(-q/2-Sqrt(QQ)))/3);
if -q/2-Sqrt(QQ)=0 then y2:=0;
x1:=y1+y2-B/A/3; Re:=-(y1+y2)/2-B/A/3; Im:=(y1-y2)*Sqrt(3)/2;
Edit8.Text := FloatToStr(x1);
Edit9.Text := FloatToStr(Re)+' + i * '+FloatToStr(Im);
Edit10.Text:= FloatToStr(Re)+' - i * '+FloatToStr(Im);
end;
· Если дискриминант равен нулю:
if QQ=0 then begin
if q<0 then y1:=exp(ln(abs(-q/2))/3);
if q>0 then y1:=-exp(ln(abs(-q/2))/3);
if q=0 then y1:=0;
x1:=2*y1-B/A/3; x2:=-y1-B/A/3; x3:=-y1-B/A/3;
Edit8.Text := FloatToStr(x1); Edit9.Text := FloatToStr(x2);
Edit10.Text:= FloatToStr(x3);
end;
В программе также организован программный контроль ввода коэффициентов. Для этого создан обработчик события KeyPress для соответствующих элементов типа Edit [6]:
if not (Key in ['-', '1'..'9', #8]) then Key := #0.
Заключение
В рамках проведенного исследования было рассмотрено несколько способов решения кубических уравнений, в том числе, с использованием формулы Кардано. Были изучены различные нюансы применения этого метода, а также проведено исследование зависимости получаемых результатов от знака кубического дискриминанта. В статье также приведен подробный алгоритм, разработанный авторами статьи, на основе тригонометрической интерпретации формулы Кардано, а также рассмотрены основные процедуры созданного программного обеспечения в объектно-ориентированной среде Delphi.
Существует довольно много проблем в различных научных областях, решение которых сводится к изучению методов решения уравнений третьей и выше степеней. Таким образом, можно сделать вывод, что актуальность проведенного исследования заключается в практическом применении рассмотренных методов, а также созданного программного обеспечения как при изучении некоторых тем математики, физики в школе и ВУЗах, так и при решении прикладных задач из различных областей.
Литература
1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. – М.: Наука, 1986.
2. Омельченко В.П., Э.В.Курбатова. Математика: учебное пособие. – Ростов н/Д.: Феникс, 2005.
3. Пичурин Л.Ф. За страницами учебника алгебры. – М.: Просвещение, 1990.
4. Корн Г., Корн Т. Справочник по математики для научных работников и инженеров. – М.: Наука, 1973.
5. Фленов М.Е. Библия Delphi. – С-Пб: БХВ-Петербург, 2011.
6. Архангельский А.Я. Delphi 7. Справочное пособие. – М.: Бином, 2004.
Поступила в редакцию 07.04.2014 г.