Анализ напряженного состояния токонесущих ортотропных оболочек в нестационарном магнитном поле
Индиаминов Равшан Шукурович,
кандидат физико-математических наук, доцент,
Хайриев Элер Ибрагимович,
Каримова Гавхар,
магистранты.
Самаркандский филиал Ташкентского университета информационных технологий, Самарканд, Узбекистан.
В работе построена нелинейная двумерная модель магнитоупругости электропроводящей оболочки с учетом конечной ортотропной электропроводности, магнитной и диэлектрической проницаемости. Проводится анализ электромагнитных эффектов и напряженно–деформированного состояния электропроводящей ортотропной оболочки с учетом ортотропной электропроводности в геометрически нелинейной постановке.
Ключевые слова: оболочка, магнитное поле, магнитоупругость.
A two-dimensional variant of connected nonlinear equations of electrodynamics of the current-carrying orthotropic rotation shells, under no stationary loads in presented. A procedure for solution of asymmetrical problems of magneto elasticity of flexible current-carrying orthotropic rotation shells under no stationary actions of mechanical and electromagnetic forces is plotted. A stress-strained state of flexible current-carrying orthotropic rotation shells in geometrically nonlinear statement.
Keywords: shell, magnetic field, magneto elasticity.
Введение
Важное место в механике сопряженных полей занимают вопросы изучения движения сплошной среды с учетом электромагнитных эффектов. Задачи электромагнитоупругости анизотропных пластин и оболочек, обладающих анизотропной электропроводностью, представляет научный интерес, как с точки зрения теории, так и приложений. В настоящей работе на примере гибкой токонесущей ортотропной конической оболочки в осесимметричной постановке, находящейся в магнитном поле, исследуется влияние учета нелинейности при определении напряженно-деформированного состояния токонесущих ортотропных пластин и оболочек в геометрически нелинейной постановке. Большинство известных работ по деформированию упругих проводящих тел выполнены для линеаризованной системы уравнений. Однако, решение ряда прикладных задач, к которым нужно отнести нестационарные задачи определения напряженного состояния гибких токонесущих анизотропных оболочек, требует более полного изучения механических процессов, включая волновые поля, сопровождающие магнитоупругое взаимодействие, на основе нелинейной модели магнитоупругости и представляют собой актуальную научную задачу.
Связанная разрешающая система нелинейных магнитоупругих уравнений в частных производных восьмого порядка, описывающая напряженно-деформированное состояние гибких токонесущих ортотропных конических оболочек обладающей ортотропной электропроводности в переменном магнитном поле, а также методика решения такого нового класса задач изложены в [1], где связанная система уравнений электродинамики получена в лагранжевых переменных, отнесенных к недеформированной срединной поверхности оболочки в ортогональной криволинейной системе координат.
Нелинейная постановка задачи
Рассматриваем гибкую токонесущую бороалюминиевую
коническую оболочку в осесимметричной постановке, находящуюся во внешнем
магнитном поле 
под действием нормальной поверхностной
нагрузки 
. К контурам оболочку подводится сторонний
электрический ток плотности 
, а также оболочка
имеет конечную ортотропную электропроводность 
.
Считаем, что сторонний электрический ток в невозмущенном состоянии равномерно
распределен по оболочке, т.е. плотность стороннего тока не зависит от
координат. Контур малого радиуса 
свободен в нормальном
направлении, а второй контур 
– жестко закреплен.
Для эффективного использования предложенной методики
[2] предполагаем, что при появлении внешнего магнитного поля не возникает
резких скин-эффектов по толщине оболочки. Отметим, что в рассматриваемом случае
произвольная поверхность второго порядка обладает тремя взаимно перпендикулярными
осями второго порядка и можно расположить эти оси параллельно
кристаллографическим осям второго порядка, а также характеристическая
поверхность второго порядка обладает всеми элементами симметрии, которые могут
быть у классов орторомбической системы. Для получения устойчивого процесса
счета введем замену 
, где 
-
безразмерная плотность. В такой постановке система уравнений, описывающая на
соответствующем временном слое нелинейные колебания гибкой токонесущей
ортотропной конической оболочки, согласно [1-4], после применения метода квазилинеаризации
принимает вид
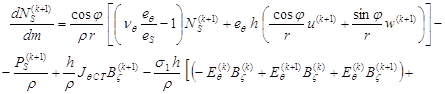
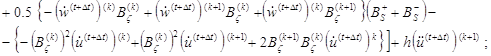
(1)
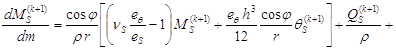
Выбирая в качестве независимой переменной длину
образующей конуса 
, величины,
характеризующие геометрию оболочки, выразятся формулами
.
В этом случае граничные условия запишем в виде
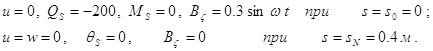(2)
Начальные условия принимают вид
. (3)
Здесь 
меридиональное и
окружное усилия; 
сдвигающее усилие; 
перерезы-вающее усилие; 
изгибающие моменты; 
перемещение и прогиб; 
угол поворота нормали; 
компоненты механической нагрузки; 
-окружная составляю-щая напряженности
электрического поля; 
-нормальная составляющая
магнитной индукции; 
-известные составляющие
магнитной индукции из поверхности оболочки; 
-составляющая
плотности электрического тока от внешнего источника; 
–
модули упругости по направлениям 
-соответственно; 
-коэффициенты Пуассона, характери-зующие
поперечное сжатие при растяжении в направлении осей координат; 
магнитная проницаемость; 
круговая частота; 
–главные
компоненты тензора удельной электропроводности. При решении задачи параметры
принимают следующие значения:
, 
, 
, 
, 
, 
, 
, 
, 
,
, (4)
, 
,
, 
,
.
Исследованы напряженно-деформированные состояния
гибких оболочек в нелинейной постановке на основе сравнения результатов
решений, полученных для токонесущего ортотропного конуса из бериллия и токонесущего
изотропного конуса из алюминия, а также для изотропного конуса из алюминия при
отсутствии магнитного поля и стороннего тока. На рисунках 1 и 2 показаны
изменения нормального и тангенциального составляющих сил Лоренца 
и 
в
зависимости от времени при 
для вариантов: 1 -
изотропный конус из алюминия; 2 - ортотропный конус из бериллия. Из рисунков
видно, что максимальные значения составляющих сил Лоренца возникают при
значении 
, причем, нормальные составляющие по
сравнению тангенциальных в 1,5 -2,0 раза больше для изотропного конуса из
алюминия, а в случае ортотропного конуса из бериллия в 6,5-7,0 раз.
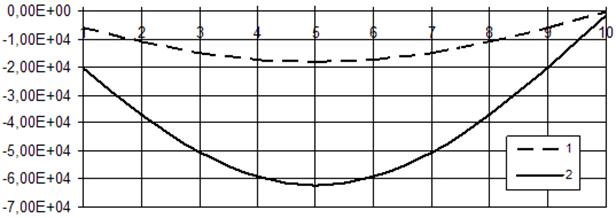
Рис. 1. Распределение 
при 
для вариантов.
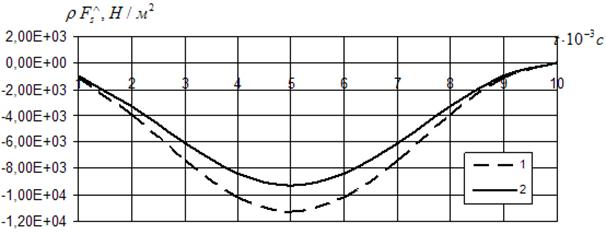
Рис. 2. Распределение 
при для вариантов.
Полученные результаты показывают влияние ортотропной электропроводности, стороннего электрического тока и внешнего магнитного поля на напряженно-деформированное состояние оболочки, а учет геометрической нелинейности позволяет существенно уточнить картину деформирования.
Литература
1. Мольченко Л.В, Лоос I.I., Индиаминов Р.Ш. Магнiтопружнiсть конiчноi оболонки з врахуванням ортотропноi электропровiдностi в геометрично нелiнiйнiй постановке // Вiсник Киiвского Унiверситету. Серiя: фiзико-математичнi науки. -2007. Вип. -№2. -С. 85-90.
2. Мольченко Л.В., Лоос И.И., Индиаминов Р.Ш. К определению напряженного состояния гибких ортотропных оболочек вращения в магнитном поле // Международный научный журнал «Прикладная механика». - 2008. - № 8 (44). - С. 64-76.
3. Индиаминов Р.Ш. Об отсутствии влияния тангенциальной составляющей силы Лоренца на осесимметричное напряженное состояние токонесущей конической оболочки // Вычислительные технологии. - Новосибирск. - 2008. - № 6 (13). - С. 66-78.
4. Индиаминов Р.Ш. Решение связанных динамических задач магнитоупругости токонесущих ортотропных конических оболочек // Сборник статьей Одиннадцатой междунар. научно-практ. конф. «Фундаментальные и прикладные исследования, разработка и применение высоких технологий в промышленности». 27-29 апреля 2011 г., г. Санкт-Петербург, Россия. Т. 3. - Санкт-Петербург, 2011. - С: 152-158.
Поступила в редакцию 03.04.2014 г.