К вопросу теоретического исследования интеллектуальных вибровозбудителей с низкой механической частотой колебании

 

Мамедов Фирудин Ибрагим оглы,

доктор технических наук, профессор, заслуженный деятель науки, член корр. Национальной Академии Наук Азербайджана,

Гудретли Ильгама Рафик кызы,

докторант Азербайджанского научно-исследовательского и проектно-изыскательского института энергетики.

 

On the issue of the theoretical study of intelligent exciters with low mechanical vibration

 

Mamedov F.I.,

professor,

Qudretli I.R.,

doctorates.

The Republic of Azerbaijan, Sumgait State University.

 

На практике в технологических линиях часто применяются однофазные интеллектуальные вибровозбудители электромагнитного типа для перемещения и разделения различных изделий. Схема дифференциальное уравнения второго порядка найдено выражением тока и сила притягивания выражения в виде синусоидальной функции.

Ключевые слова: индуктивность, сила притягивания, сопротивление, емкости колебательного контура.

 

In practice, often used single-phase intelligent vibration exciters electromagnetic type for moving and separating the different products and technological line. Scheme of second order differential equations found expression current and power of attraction in the form of a sinusoidal function.

Keywords: inductance, the power of attraction, resistance, capacitance oscillation circuit.

 

Повышенные технико-экономические показатели и надежность в работе не возможны без создания низких механических колебании (НМК). Поэтому электромагнитные вибровозбудители надо создавать на основе решения теоретических уравнений равновесия. Рассматриваемый объект исследования – электромагнитная система питается от источника синусоидального напряжения, состоит из последовательной обмотки с емкостью С.

Переменная индуктивность L и постоянное активное сопротивление R обмотки, намотанной на цилиндрический стакан со средним выступом и сердечником, изготовленным из конструкционной стали. Получили интегро-дифференциальное уравнение и после дифференцирования по времени имеем 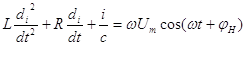[1].

                                                                    (1)

где L – индуктивность, С – емкость колебательного контура, R – активное сопротивление обмотки возбуждения,  - угловая частота питающего напряжения, U_m –амплитуда напряжения, φ_н – сдвиг фаз напряжение. Решая полученное уравнение (1) получим:

                                                                                                   (2)

где , φ_i – соответственно постоянного интегрирования. Для определения этих интегрирований с учетом (2) получим:

          (3)

 

Раскрывая тригонометрическое преобразование, получим следующую систему уравнений

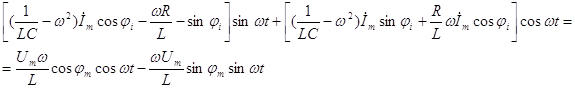 (4)

 

 

Приравнивая коэффициенты  и , составим следующую систему уравнений:

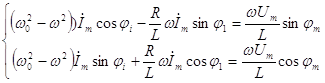                                                (5)

 

 

Решая систему уравнений (5) получим постоянного интегрированной

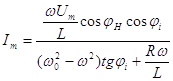                                                                                      (6)

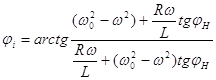                                                                           (7)

 

 

Определив из (7)  получим:

                                                                                                         (8)

 

подставим (8) в (6) и после некоторых преобразователей получим:

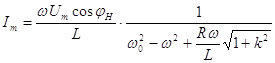                                                             (9)

 

Подставив постоянного интегрированный в формуле (2) будем имеет:

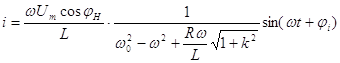                                            (10)

 

 

Полученные формулы позволяют определить силу притягивания, для этого возникает необходимость записать закон сохранения энергии, записанный в виде:

                                                                               (11)

Здесь, --изменение источника энергии, -2 -изменение количества энергии, - изменение энергии по площади, - механическая работа.

 пользуемая сила притягивания, которая записывается в виде:

                                                                                          (12)

 

Как видно из (12) выходящий состав этой формулы является не несинусоидальный. Путем исследования установлено, что одна гармоника тока соответствуют двум гармоникам силы притягивания. В связи с этим сила притягивания определяется соответственно каждое гармонике, затем они складываются. Для определения силы притягивания сначала находим первую гармонику в зависимости от . Затем определяем первую гармонику силы притягивания  ]:

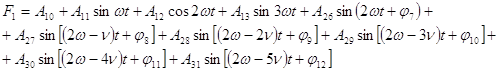     (13)

 

 

Аналогичном образом находим сила  и , а затем складываем их и получим:

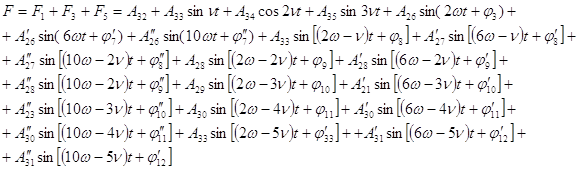  (14)

 

 

 

 

В исследовании однофазного вибровозбудителя используется индуктивной датчик на выходе, который получает синусоидальное напряжение. Временная зависимость этого напряжения близка к синусоидальности механической колебаний. Эквивалентная синусоида показывает, что действующая на якорь сила полностью повторяется с частотой [2].

Как отличено выше на выходе индуктивного датчика мы получаем модулирующую частоту. При установке на выходе датчика высокой частоты задыхается, а низкие частоты соответствуют амплитуде силы притягивание. Принимая, что к=2,6,10,…и т.д.

Сила притягивания

                                                                                                     (15)

где - эквивалентность сила притягивании и равно

                  (16)

 

Заключение

           

 Полученная формула отражает в себе все конструктивные параметры, а также позволяет конструировать вибровозбудители.

 

Литература

 

1.                  Поливанов К.М. «Теория электромагнитного поля». М.: Энергия, 1975

2.                  Зевеке Г.В., Иоркин П.А., Нетушил А.В., Страхов С.В. «Основы теории цепей» М.: Энергоатомиздат 1989.

3.                  Лосев А.К. «Теория линейных электрических цепей» М.: Высшая школа, 1987

4.                  Интернетные материалы: International Rectifier, управление питанием Дмитрий Еськин, «Использование интеллектуальных» приводов серии № А на объектах нефтяных компаний; Южная Корея в РФ и странах СНГ.

 

Поступила в редакцию 24.06.2015 г.