О повышении точности измерителя флуктуаций частотно-модулированных сигналов

 

Еникеев Александр Фанилович,

доцент Краснолиманского филиала Украинского государственного университета железнодорожного транспорта.

 

Введение

 

При разработке средств автоматизации процессов алмазного шлифования (АШ) нашел применение метод оценивания качества обработанной детали по девиациям скорости вращения круга [1]. Измерительная информация заложена во флуктуациях периодов выходного сигнала датчика. Аппаратные средства обработки частотно-модулированного сигнала состоят из датчика, измерительного преобразователя (ИП) и вычислительного устройства.

Целью статьи является разработка эффективных аппаратных средств измерений флуктуаций частотно-модулированных сигналов. Достижение поставленной цели выполняется путем решения следующих задач:

·                    разработка математической модели процесса АШ;

·                    выработка требований к метрологическим характеристикам ИП;

·                    реализация эффективных аппаратных средств.

 

Разработка модели процесса алмазного шлифования

 

Режимы резания поверхности заготовки задают поперечная и продольная подачи шлифовального круга (ШК). Используем эти параметры процесса АШ в качестве входных сигналов разработке его математической модели. Выходной сигнал - сила резания поверхности заготовки. С учетом динамики процесса резания, упругих деформаций станка и линейного износа ШК в работе [1] получено выражение для передаточной функции

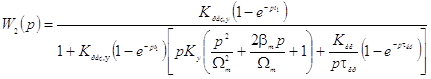,                     (1)

 

 

где  – коэффициент резания по координате S_поп, K_y – статическая жесткость станка, b_m – коэффициент демпфирования станка,  – коэффициент износа инструмента,  – время оборота,  – время прямого или обратного хода, W_m – резонансная частота конструкции станка. Выражение (1) связывает поперечную подачу ШК с радиальной составляющей силы резания.

С учетом динамики процесса резания и упругих деформаций станка в работе [1] получено выражение для передаточной функции, которая связывает продольную подачу ШК с тангенциальной составляющей силы резания

,                                                                               (2)

 

где  – коэффициент резания по координате x (S_пр), K_x – статическая жесткость конструкции станка.

Входной сигнал модели с учетом прямого и обратного хода ШК представлен так (для продольной подачи ШК аналогично)

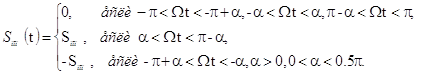                     (3)

 

 

Радиальная и тангенциальная составляющие силы резания материала заготовки ортогональны. На основе линейности преобразования Лапласа и с учетом теоремы сложения получено уравнение для суммирования указанных составляющих силы резания

.                                                                   (4)

Сила резания материала заготовки создает возмущение, которое является источником крутильных колебаний. Вал вместе с ШК представлен механичной системой с одной степенью свободы. Движение массы описывает дифференциальное уравнение второго порядка

,                                                                           (5)

где  – момент инерции ШК,  – коэффициент демпфирования,  – крутильная жесткость вала,  – возмущение.

После выполнения процедуры нормализации и преобразований получена передаточная функция, которая связывает сигнал флуктуаций и силу резания материала заготовки

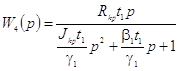.                                                                                                (6)

 

 

По выражениям (1), (2), (4) и (6) составлена схема имитационного моделирования процесса АШ (рис. 1). Получен график флуктуаций (рис. 2).

 

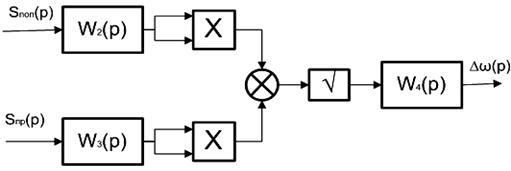
Рис. 1. Структурно-логическое построение модели процесса АШ.

 

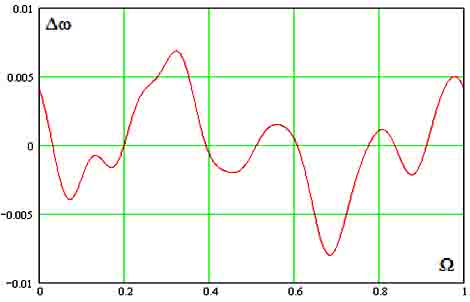
Рис. 2. Выходной сигнал модели.

 

Установлено, что глубина модуляции частотно-модулированного сигнала не превышает 0.05. Поэтому процедура измерений флуктуаций требует разработки высокоточных методов и соответствующих аппаратных средств.

 

Информационно-измерительное устройство

 

Разработка устройства начата с анализа составляющих погрешности первичного преобразователя (ПП):

·                    ошибка восстановления аналогового сигнала по дискретным отсчетам, которая получена для его частотного представления в таком виде [2]

,                                                                                          (7)

 

где  – соответственно интервал дискретизации и угловая гармоника частотного представления входного сигнала;

·                    кинематическая ошибка ПП, которая установлена на примере исследований допусков на изготовление зубчатых колес различного класса точности [2]. Результаты оценивания представлены в табл. 1

,                                                                                                         (8)

 

где  – допуск на изготовление зубчатого колеса, заданного класса точности,  – модуль;

·                    динамическая погрешность ПП.

 

Таблица 1.

Расчетные данные кинематической погрешности.

Класс точности ПП	4	5	6	7	8
, %	0.80	1.25	2.00	2.75	4.00
Ошибка измерений флуктуаций, %	16.0	25.0	40.0	55.0	80.0

 

Данные табл. 1 позволяют сделать вывод: проблема измерений флуктуаций частотно-модулированных сигналов состоит в разработке аппаратных средств для уменьшения величины кинематической погрешности. Автором предлагается метод многоканальных измерений длительностей интервалов времени, которые соответствуют одному обороту вала датчика и формируются одним отметчиком. При этом кинематическая погрешность не влияет на длительность сформированного измерительного интервала. Она находит проявление в смещениях во времени дискретных отсчетов временной реализации сигнала флуктуаций. Установим динамическую погрешность смещений по времени дискретных отсчетов выходного сигнала имитационной модели (рис.2). Представляем этот сигнал в виде ограниченного ряда Фурье. Ее абсолютное значение оценим следующим образом [1]

,                                                                                    (9)

 

где  – количество отметчиков ПП.

С точностью до величины второго порядка малости относительно динамической погрешности сумму заменим интегралом

.                                                                   (10)

 

Для гармонического сигнала последнее выражение после преобразований приобретает вид

.                                                               (11)

 

Отсюда, относительное значение динамической погрешности гармонического сигнала имеет такой вид

.                                                                       (12)

 

Динамическую погрешность ПП определим с учетом вкладов гармонических составляющих в сигнал флуктуаций

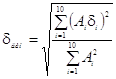.                                                                                                    (13)

 

 

Результаты расчета динамичной погрешности, которая присуща ПП, представлены в табл. 2. Данные таблиц 1 и 2 позволяют сделать заключение о корректности предложенного метода, который компенсирует кинематическую погрешность изготовления ПП.

 

Таблица 2.

Результаты расчета динамической погрешности.

Класс точности	4	5	6	7	8
Погрешность измерений флуктуаций, %	3.1	4.8	7.4	9.9	14.1

 

Метод измерений флуктуаций частотно-модулированного сигнала состоит в следующем. Посредством счетчика и дешифратора выходной сигнал ПП преобразуется в определенное количество сигналов, измерительная информация которых заложена в длительности интервалов между импульсами. Количество сформированных сигналов и, соответственно, каналов для измерений длительности определяется числом отметчиков ПП. В основу построения каналов для измерений длительности положен метод дискретизации по времени. Устранение наложений выходных сигналов каналов при формировании сигнала измерительной информации выполняют счетчики. Их объем и частота квантующего генератора подобраны таким образом, чтобы переполнение счетчика выполнялось за время, которое меньше чем средний период импульсных последовательностей. В этом случае из выходных сигналов каналов исключается калиброванный по длительности интервал времени. Разность между поточным измеряемым интервалом и калиброванным представляет собой выходной сигнал канала. Объединение выходных сигналов каналов в сигнал измерительной информации выполняется посредством логической схемы ИЛИ.

Структурно-логическое построение ИП представлено на рис. 3 [3]. ИП содержит: генератор (Г); делитель частоты (ДЧ); дешифратор (ДШ); два счетчика импульсов (СЧ3 и СЧ4); устройства для измерений длительности, причем их количество равно числу прорезей диска; две схемы ИЛИ (ИЛИ1, ИЛИ2); одновибратор (Ф) и линию задержки (ЛЗ). Каждый блок состоит из: четырех схем совпадения (И1,...,И4), двух счетчиков импульсов (СЧ1, СЧ2) и трех триггеров (Т1,…,Т3). На рисунке также обозначено: N_x – измерительная информация, упр – сигнал записи.

 

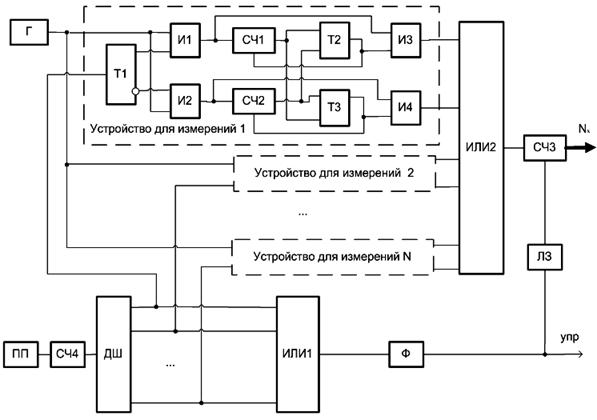
Рис. 3. Структурно-логическое построение ИП.

 

Анализ эффективности измерительного преобразователя

 

Выполнена статистическая обработка экспериментальных данных. На рис. 4 представлена гистограмма разброса выходного кода. Объем выборки составил 151 измерение. Основные статистические параметры следующие

, , , .

 

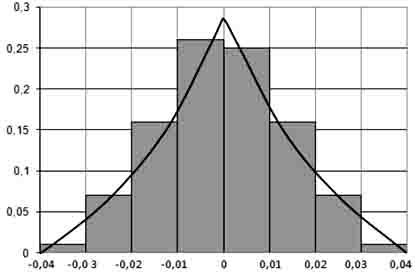
Рис. 4. Гистограмма разброса выходного кода ИП.

 

Гистограмма разброса выходного кода после выполнения процедуры сглаживания описана экспоненциальным законом распределения, который по виду достаточно близкий к треугольному. Уравнение сглаженной кривой

 при .                                                                    (14)

 

На основе информационного подхода установлен энтропийный интервал неопределенности ИП

.

 

Выводы

 

Усовершенствована математическая модель процесса АШ, которая отличается двухмерным структурно-логическим построением. Входные сигналы модели задаются поперечной и продольной подачами ШК, последующее ортогональное суммирование обеспечивает получение выходного в виде сигнала флуктуаций. В результате анализа сигнала флуктуаций сформулированы требования по точности для ИП. Впервые предложен метод измерений флуктуаций частотно-модулированного сигнала, отличающийся применением аппаратных средств компенсации кинематической погрешности изготовления ПП. Разработан измеритель флуктуаций частотно-модулированного сигнала и установлена его эффективность.

 

Литература

 

1.                  Еникеев А.Ф. Оптимальное управление технологическим процессом алмазного шлифования. – Краматорск: ДГМА, 2001. – 160 с.

2.                  Допуски и посадки. Справочник. / [Гл. ред. Мягков В.Д.] - Л.: Машиностроение, Часть 2, 1978. - с. 545-1032.

3.                  А.с. № 1538679 (СССР). Устройство для контроля неравномерности вращения вала / Марченко Б.Г., Борисенко А.Н., Еникеев А.Ф.

 

Поступила в редакцию 16.01.2015 г.