О бесконечности числа регулярных простых чисел
Карпунин Иван Иванович,
доктор технических наук, профессор, профессор кафедры Белорусского национального технического университета, академик МИА.
Теорема. Если 
–
иррегулярное простое число, равное 
(p>37), то между p и
содержится по меньшей
мере одно регулярное число V, равное 
.
Доказательство. Из литературы [1-5] известно, что число иррегулярных простых чисел бесконечно. Докажем, что число регулярных простых чисел также бесконечно.
Так как 
, то целое 
(где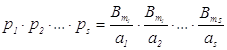 
, 
– числители чисел Бернулли, 
– целые числа после деления 
на 
),
очевидно >1.
Предложение. Если 
делится
на 
, то
независимо от того 
дробное или целое число ≥1,
деление на это число дает целое число.
Итак имеем II случая: 
может
быть целым или дробным числом: 
– целым, 
дробным большим 1.
Частный случай I: 
–
целое число. Итак имеем 
. Если делится
на 
, то получается целое число, допустим 
. Тогда 
, где 
.
Частный случай II. Здесь 
, 
– дробное число >1. Представим дробное
число следующим образом 
. Тогда 
, 
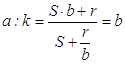. В обоих случаях имеем сравнение по
ненулевому рациональному модулю.
В связи с тем, что 
(независимо
от того 
– дробное или целое число >1, как
частные случаи деления 
на 
), оно
имеет делитель, который <
, а следовательно, и
<
. Если допустить, что 
, то 
будет одним
из сомножителей произведения: 
(где может быть целым, или дробным числом
>1, как частный случай 
) и значит будет
делителем произведения . Но будучи делителем
также числа , будет
делителем разности этих чисел, или числа 
, что
невозможно, так как 
и 
.
Следовательно, 
, а так как уже выяснено, что 
, то имеем 
.
Так как 
, 
, …,
(где 
, 
,…,
– также делители чисел ) и последовательность иррегулярны простых
чисел бесконечна, то получим последовательность простых регулярных чисел: 
количество которых также бесконечно. Это
означает, что теорема доказана.
Таким образом, для каждого иррегулярного числа существует регулярное большее его. Отсюда следует, что простых регулярных чисел бесконечное множество. Обобщая вышеизложенное и литературные источники [1-5] предлагается следующее.
1.
Доказать, что уравнение: 
не имеет решения в целых числах при 
.
2.
Доказать, что уравнение: 
не делится на 
(
;
).
3.
Доказать, может ли данное простое 
делить число вида: 
, где 
-
данное целое, а 
и 
-
взаимно простые целые числа (
).
4. Доказать, что в любых арифметических прогрессиях (1) и (2):
(1)
(2)
для которых и взаимно простые числа, содержится
бесконечно много простых чисел.
5.
Доказать, может ли уравнение: 
иметь решения в целых числах (
- простые числа, 
,).
6.
Доказать, может ли уравнение 
имеет решения в целых числах
(
, 
).
7. Доказать, что существует бесконечное множество значений n, при которых число 2 + n простое, где n простое нечетное число.
8. Доказать, что существует ли бесконечное множество значений x и n при которых число хn + 2 простое, где n и х – простые числа при n=х и при n≠x.
9.
Доказать, имеют ли решения в целых
числах уравнения: хn +xn-1 .y=Zn ; xn +xn-1.y
+xn-2 .y2 =zn ;…; xn +xn-1.y
+xn-2 .y2 +….+yn-2x2+yn-1x
+yn=zn , где n≥3, n-простое нечетное число, (уравнение xn +xn-1.y
+xn-2 .y2 +….+yn-2x2+yn-1x
+yn=zn имеет решение в целых числах при n =2 и
х=5, у=3).
10. Доказать, имеют ли решения в целых числах уравнения: хn +nxn-1 .y=zn;
n(n-1)
xn +nxn-1.y + ─ xn-2 .y2 =zn ;….; хn +nxn-1 .y+ …+ nyn-1x=zn ,
1.2
где n –простое число, n≥3, .
11. Доказать, существует ли бесконечное значений n, при которых числа 2n +1 и 2n-1 одновременно составные (например, 2n +1 делится на3, 2n-1 делится на 23 при n=11).
12. Доказать, имеет ли решение в целых числах
уравнение xn +xn-1.y +xn-2 .y2 +….+yn-2x2+yn-1x
+yn=zm , где m≠n , m,n≥3, , .
13. Доказать, имеет или не имеют решений в целых числах уравнения mn + mn + nn =pk ; mm +mn + nn =pk ; mn +mn + nn =pn , где k,m,n,p ≥3 –простые числа.
14. Доказать, имеет ли решения в целых числах уравнение xm +yn +zp =tk, где m≠n≠p≠k, x≠y≠z≠0, m,n,p,k≥5- простые нечетные числа.
Литература
1. Боревич З.И., Шафаревич Н.Р.Теория чисел. М.: Наука.–1985.368 с.
2. Постников М.М. Введение в теорию алгебраических чисел. М.: Наука – 1980. –– 239 с.
3. Эдвардс Г. Последняя теорема Ферма. М.: Мир.–1980.– 480 с.
4. Айерленд К., Роузен М. Классическое введение в современную теорию чисел. М.: Мир – 1987 – С. 295.
5. Карпунин И.И., Подлозный Э.Д. К вопросу о делимости чисел / Сучаснi проблеми науки та освiти. 8-а Мiжнародна мiждисциплiнарна науково-практична школа-конференцiя. Харькiв – 2007. – С. 80.
Поступила в редакцию 09.02.2015 г.