Условия существования неподвижных точек операторов вольтерровского типа с периодическими коэффициентами
Исмоилов Хамроли Канбарович,
старший преподаватель Андижанского машиностроительного института, Узбекистан.
Операторы вольтерровского типа определяются равенствами:
(1)
где 
- непрерывные функции, удовлетворяющие
условиям:
а) 
, для любого 
,
б) 
, для всех .
Легко
заметить, что при выполнении этих условий 
[1].
Интересным с
биологической точки зрения является случай, когда 
-параметры
управляющие эволюцией, являются периодическими функциями [2].
В настоящей
работе изучается вопрос о существовании и количестве неподвижных точек
операторов вольтерровского типа с периодическими коэффициентами. В качестве берутся периодические функции 
и 
.
В симплексе 
рассмотрим семейства квадратичных
стохастических операторов вида:
где 
Теорема 1.
Для любых 
квадратично-стохастических
операторов число всех неподвижных точек равно 
Доказательство. Решим систему
Если 
, то 
, и
, где 
. Следовательно,
и при 
, получаем
неподвижную точку. Очевидно других
неподвижных в 
точек нет.
В симплексе 
рассмотрим семейство квадратичных
стохастических операторов вида:
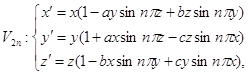(2)
где 
Очевидно, 
, кроме того, все точки 
, неподвижны относительно 
. Кроме того 
и 
квадратично-стохастические
операторы имеют единственную внутреннюю отталкивающую неподвижную точку 
. Легко заметить, что 
имеет не менее четырех, а 
не менее семи внутренних неподвижных
точек.
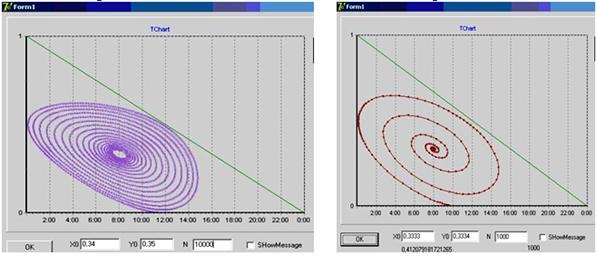
Рис. 1. n = 1. Рис. 2. n = 2.
Теорема 2.
Если 
тогда:
1)
Все точки неподвижны;
2)
-внутренняя отталкивающая неподвижная
точка;
3)
Существует 
внутренних неподвижных точек 
Доказательство.
1) Очевидно, что все точки неподвижны.
2) Легко
заметить, что внутренняя отталкивающая
неподвижная точка(рис.1, рис.2, рис.3,…).
3) Решим систему
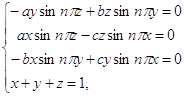
полученную из (2).
Эта система
имеет место при всех комбинациях точки 
,
здесь 
, и 
Число решений
уравнения 
в целых неотрицательных числах
и 
, равно
.
Пусть 
и 
тогда,
-внутренняя отталкивающая неподвижная
точка.
Допустим, что центр симплекса является внутренней неподвижной точкой. Тогда верно следующее утверждение.
Утверждение.
Если тогда:
1)
Все точки неподвижны;
2)
Существует 
внутренних неподвижных точек
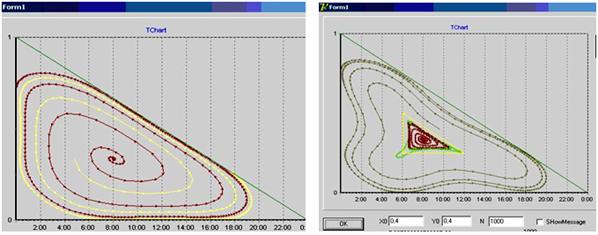
Рис. 3. n = 3. Рис. 4. n = 4.
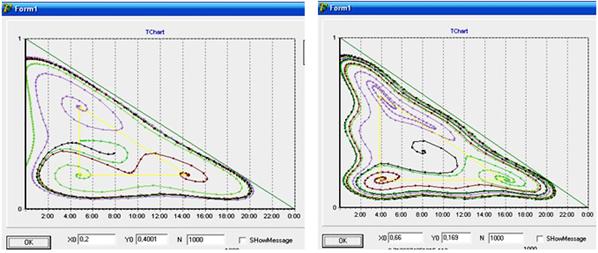
Рис. 5. n = 5. Рис. 6. n = 6.
Рассмотрим семейство квадратичных стохастических операторов вида:
в симплексе , где
Теорема 3.
Для любых 
квадратично-стохастических
операторов число всех неподвижных точек равно 
Доказательство. Решим систему
Если 
, то 
Здесь 
. Число целочисленных решений уравнения в нечетных числах 
и
равно 
.
Тогда число неподвижных точек равняется:
и две вершины
симплекса 
и 
.
Итак, мы
показали, что число всех неподвижных точек равно 
.
В симплексе рассмотрим семейство квадратичных
стохастических операторов вида:
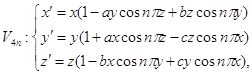(3)
где 
Очевидно, 
, кроме того, вершины 
и 
являются
неподвижными точками.
Теорема 4.
Пусть тогда:
1) -внутренняя отталкивающая неподвижная
точка;
2) Существует
неподвижных точек которые лежат на ребрах
симплекса 
.
Доказательство.
1) Из рис.7, рис.8, рис.9 и рис.10 видно, что траектория 
точек имеет спиральный вид. Это означает,
что внутренняя отталкивающая неподвижная
точка.
2) Решим систему
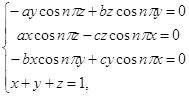
полученную из (3).
Эта система
имеет место при всех комбинациях точки 
, 
,
, здесь
, и 
Из 
видно, что по теореме 3 существует равно 
неподвижных точек принадлежащих ребру 
симплекса .
Отсюда
находим, что число неподвижных точек находящихся на ребрах равно .
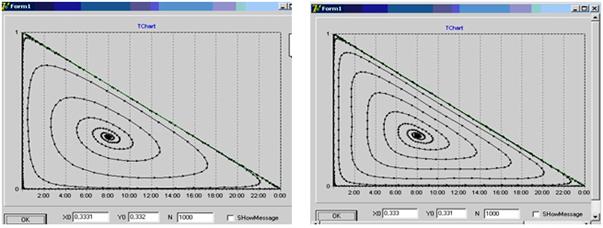
Рис. 7. n = 1. Рис. 8. n = 2.
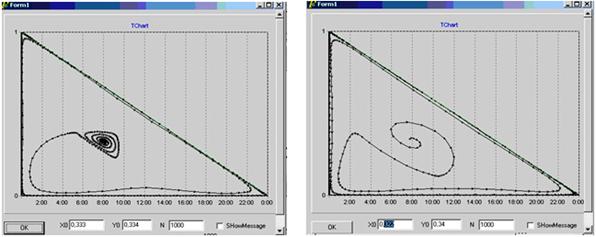
Рис. 9. n = 3. Рис. 10. n = 4.
Литература
1. Ганиходжаев Р.Н. Квадратичные стохастические операторы, функция Ляпунова и турниры. Математический сборник, 1992 г., т.183, №8 с.129-141.
2. Ганиходжаев Р.Н. Исследования по теории квадратичных стохастических операторов // Автореф. доктор. дис.., Ташкент, 1994 г.
3. Курганов К.А. Асимптотическое поведение траекторий дискретных динамических систем, порожденных квадратичными стохастическими операторами вольтеровского типа // Автореф. канд. дис., Ташкент,1994 г.
4. Г.Полиа, Г.Сеге. «Теорема и задачи в анализе» том I,II, Москва: Наука, 1978 г.
Поступила в редакцию 19.02.2015 г.