О разности между последовательными простыми числами

 

Лукашов Валерий Леонидович,

генеральный директор общества с ограниченной ответственностью «Авеста».

 

Используя известные математические знания и приемы, исследовать разность между последовательными простыми числами и, доказав гипотезу Римана без использования комплексных чисел, установить минимальное на данный момент значение и графическое место расположение этой разности при стремлении простых чисел к бесконечности.

Ключевые слова: простое число, подмножество простых чисел, прогрессия убывающая, функция.

 

Изучается графическое положение разности между последовательными простыми числами при стремлении простых чисел к бесконечности.

 

1. Введение.

При любых числах  всегда существуют число , множество  и объединение множеств . Поэтому и по теореме Чебышева [2, гл.1, c.14], для любого простого числа  всегда есть такое число , что . Следовательно, существуют непустые множества:

, , .

Так как множество простых чисел , то для любых последовательных чисел  всегда существует число  и число . Тогда, при любых числах  всегда существуют числа

.

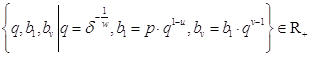Так как по теореме Чебышева , то - геометрическая убывающая последовательность, где  - первый член , а  - знаменатель .

Так как , то в любой  

, .                                                                                                     (1)

Так как логарифмы элементов  есть элементы последовательности  арифметической, то

, .                                                          (2)

 

2. Промежуточные результаты.

Если , то существуют убывающая функция  и обратная ей убывающая функция :

.                                               (3)

Если , то существуют убывающая функция  и обратная ей убывающая функция :

                                                        (4)

Согласно свойствам, графики  и  пересекаются на биссектрисе первого координатного угла в точке . Тогда , откуда

, .                                                                                       (5)

Согласно свойствам, графики  и  пересекаются на биссектрисе первого координатного угла в точке . Тогда , откуда

, .                                                                                            (6)

Согласно свойствам, график  пересекает только раз только ось , график  - только ось , а графики  и  - по разу и , и :

 , .

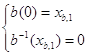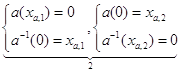Поэтому и так как (5) и (6) однозначно выражают  через  и наоборот, то решив любую одну из систем, систему 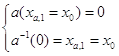, получим

, .                                                                                                           (7)

Так как (2) и (7), то , откуда

. (8)

Так как (2) и (7), то , откуда

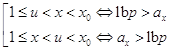, . (9)

Так как (2) и (6), то , откуда .

Применив  и (9), получим

.

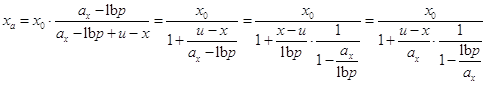Применив , получим

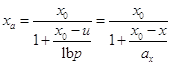.                                                                                      (10)

 

 

3. Доказательство теоремы.

Используя введенные обозначения и полученные результаты, докажем следующие утверждения.

Лемма 1: если , , , то .

Доказательство. Так как (3) и (4), то, откуда .

Так как (8), то , откуда числа , когда .

Тогда и так как , то , откуда . Доказано.

Лемма 2: если , то .

Доказательство - случай 1: .

Если , то , откуда . Поэтому и так как (10), то

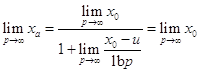. Доказано.

 

Доказательство – случай 2: .

Если, то  и , откуда . И так как (10), то

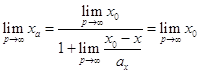. Доказано.

 

Лемма 3: если , то  для любого .

Доказательство. Если , то , откуда для любых  всегда есть такое , что . Тогда, по теореме Евдокса–Архимеда, [1, гл.I, §2, п.7, сл.3], всегда существует такое число , что

.

Поэтому и так как , то

.                                                                                  (11)

Случай 1: . Пусть , пусть .

Если (11) и Случай 1, то , откуда

.

Следовательно,

.                                                                      (12)

Если Случай 1 и так как (9), то , откуда. Тогда и так как  и  при , то всегда существует такое , что

.                                                                                              (13)

Если (12) и (13) и так как , то , откуда

.

Следовательно,

. Доказано.

Случай 2: . Пусть , пусть .

Если (11) и Случай 2, то , откуда

.

Следовательно, , откуда

.                                                  (14)

Если Случай 2 и так как (9), то , откуда . Тогда и так как  и  при , то всегда существует такое , что

.                                                                                                 (15)

Если (14) и (15) и так как, то

.

Следовательно, , откуда

. Доказано.

 

Теорема: если  и , то  стремиться к биссектрисе первого координатного угла.

Доказательство. Так как Лемма 1 и Лемма 2, то  при .

Поэтому и так как (1) и Лемма 3, то. Доказано.

Следствие: если , то  и .

Так как (8) и Теорема, то 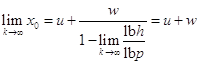, откуда .

Следовательно, . Доказано.

Если  и так как Теорема, то , откуда

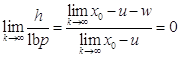. Доказано.

 

График исследуемых функций  и  при будет иметь вид:

 

 

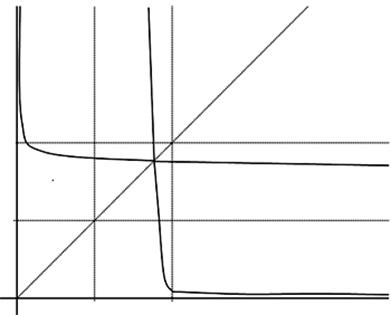
 Выводы. Доказана гипотеза Римана.

 

Литература

 

1.                  Виленкин Н.Я., Мордкович А.Г. Математический анализ. Введение в анализ. Просвещение. М: 1983.

2.                  Прахар К. Распределение простых чисел. МИР. 1967.

 

Поступила в редакцию 07.04.2015 г.