Основы общей теории неустойчивости
Скворцов Генрих Евгеньевич,
кандидат физико-математических наук, старший научный сотрудник Санкт-Петербургского государственного университета,
Перевозников Евгений Николаевич,
кандидат физико-математических наук, доцент кафедры технического обеспечения торговых и технологических процессов Санкт-Петербургского торгово-экономического университета.
В работе представлены основания общей теории неустойчивости. Они состоят из сингулярно-динамических определений неустойчивости, методов получения ряда критериев неустойчивости и ее особого режима – хаоса. Приведены примеры получения критериев для двух простых динамических моделей.
Ключевые слова: динамические системы, понятие и критерии неустойчивости, сингулярно-динамический метод, хаотичесие режимы.
1. До недавних пор приоритет имела устойчивость, ее определение и обеспечение. Она важна для технических систем и процессов, именно поэтому теория устойчивости занимала главное место, а в ней – теория Ляпунова.
Однако за последние десятилетия была признана роль неустойчивости во всех качественных преобразованиях систем. Это обстоятельство отражает синергетика, она по сути фокусируется на неустойчивости. Но при этом использовала критерии Ляпунова в противоположном их значении. Такая трактовка годится для технических систем, а для прочих недостаточна. Понятие неустойчивости значительно богаче антипода устойчивости Ляпунова. Например, определение фазовых переходов, с которыми связаны неустойчивости, осуществляется с использованием аналитических особенностей – скачка величин для переходов первого рода и скачка их производных для переходов второго. Известная теория катастроф не использует неустойчивости по Ляпунову.
Изучение сильно неравновесных процессов демонстрирует необходимость расширения понимания и определения неустойчивостей по сравнению с традиционным ( рост возмущений). Традиционное определение НУ не используется в известной теории режимов с обострением. Даже перехода к колебательному режиму известные критерии Гурвица не указывают.
Приведенные факты свидетельствуют о недостаточности традиционного понятия НУ, чтобы объединить и объяснить многообразие неустойчивостей, и побуждают к созданию общей теории.
2. Любая теория должна строиться на системной основе. Схема таковой представляется набором букв ONStLPMPr, которые означают: O – объекты теории; N – основные понятия; St – тематические разделы теории; L – система законов; P – принципы, оснащающие, законы; M – основные методы; Pr – проблемы, решаемые теорией.
Такая схема при ее развертывании с успехом использовалась для построения ряда теорий: общего естествознания, современной синергетики [5] и др.
Далее будем следовать этой схеме, а точнее собирать воедино ее составляющие, полученные ранее, начиная со статьи [1], после которой давались применения с обнаружением ряда новых режимов и эффектов. Законы неустойчивостей начали появляться в [4] и сформировались в [5]. Ряд важных аспектов теории НУ были рассмотрены в [2, 3]. Ключевой пункт теории – получение полного набора критериев общей неустойчивости и хаоса оставался открытым.
Решение этой проблемы – формирование сингулярно-динамической методики получения критериев, универсального инструментария, завершает построение основ общей теории неустойчивостей.
Такая методика является обобщением методов теории катастроф и анализа динамики с помощью локальной линеаризации
СД-методика исходит из ряда основных положений: общих определений неустойчивости [1, 2, 3], фундаментальных законов неравновесных состояний [4, 5] а также из опыта анализа многих сильно неравновесных динамических систем [6]. Авторы также использовали ряд сведений о хаотической динамике из [7].
СД-методика заключается в анализе динамической модели системы с целью получить набор аналитических условий (комплексного критерия), при выполнении которых в динамике системы будут хаотические режимы.
Общая динамическая модель имеет вид
, (1)
с начальными
условиями 
. В этой системе xi – определяющие
величины, левая часть – темп, правая – действие, π – набор параметров.
Далее будем рассматривать систему (1) как типовую, трехмерную. Известно, что
она достаточно представительна и проявляет основные особенности. Вместе с тем
на ней можно продемонстрировать все аспекты СД-методики.
Первый этап СД-методики заключается в определении особенностей – сингулярностей функции g по х и π. Таковыми являются: нули, особые точки, бесконечные значения, изломы, скачки функции g и ее производных. Такие особенности оказывают значительное влияние на динамику системы.
Они же через динамические инварианты системы выражаются в виде особенностей в фазовом пространстве.
На втором, с учетом выявленных особенностей, используем качественный анализ уравнений и предпринимаем попытку решить упрощенную систему.
Третий этап заключается в локальной линеаризации исходной системы и анализе ее динамики с учетом особенностей. Универсальными особенностями в этом случае являются спектральные. Они определяются из спектрального уравнения (СУ) и указывают на особый характер режимов. Этап завершается формулировкой условий неустойчивости, хаоса и выражений их через коэффициенты СУ.
3. Продемонстрируем СД методику на примерах.
3.1. Рассмотрим простейшую модель
(2)
Действие имеет очевидную особенность – уголок. Покажем, как она и начальное условие отражаются на динамике. Используем решение
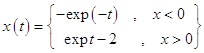. (3)
Как
показывает (3), при 
имеется одна ветвь решения, а
при 
возникает вторая. Этот бифуркационный
скачек означает физическую неустойчивость, согласно одному из ее определений [2].
Обратим внимание на роль начального условия: при 
физической
неустойчивости нет. Критерием НУ в данном случае является условие реализации
для 
двух вариантов нижней и верхней ветвей одновременно.
При этом не нужно решать уравнение. Укажем, что 
определяет
изменение фазового объема в соответствие с ее знаком, при равенстве нулю объем
сохраняется.
Далее этот простой критерий будет также использоваться.
3.2. Более содержательной является видоизмененная модель Ресслера [7] с внешним воздействием r
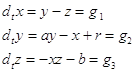, (4)
где 
- изменяющийся параметр, 
. Критерий
(5)
показывает, что имеется возможность увеличения и уменьшения фазового объема, хс=а особое значение. Прочие особенности – аналитические сингулярности: стационарные значения
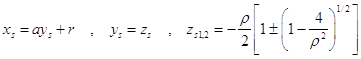(6)
. Очевидно, при 
стационарный
режим отсутствует.
-сингулярность, т.к. 
. Потенциальная сингулярность 
. Отметим, что особыми могут быть
начальные условия, как например 
.
Переходим к
анализу возмущений- линеаризованных уравнений относительно начального состояния.
Им может быть 
или стационарные состояния
(6), как обычно принимается, либо любое другое.
Динамику возмущений представляет спектральное уравнение
(7)
, нуль указывает, что величины
вычисляются в исходном состоянии. В развернутой форме для трехмерной системы СУ
принимает вид
, (8)
Выражения коэффициентов в СУ вычисляются через gi j , например
. (9)
Укажем общие особенности, которые представляет СУ:
1) смена убывания на рост- режим неколебательной нейтральности;
2) возникновение колебаний;
3) их нейтральный режим;
4) переход к хаотической динамике.
Все они определяются набором коэффициентов s,p,q , зависящих от динамических коэффициентов, величины воздействия r и исходного состояния.
Приведем условия – критерии указанных режимов соответственно
, (10)
, (11)
. (12)
Относительно хаотического режима следует сказать подробнее. Как показывает опыт численного решения трехмерных динамических уравнений с квадратичной нелинейностью критерием возникновения и существования хаотического режима является наличие линейного режима соответствующего собственным значениям
, (13)
При условии
. (14)
Такой режим называется седлофокусом. Во всех решенных задачах условия (13) оказываются необходимыми и достаточными. Для их выполнения критерии (11, 12) следует дополнить критерием разных знаков (14). Из выражения для q через собственные значения
. (15)
Следует:
(16)
Знак 
соответствует знаку комплекса
. (17)
Объединяя критерии (16) и (17) , получаем критерий седла-хаоса
. (18)
Применим полученные критерии к задаче (4). Коэффициенты СУ имеют здесь вид
. (19)
Индекс ноль
соответствует исходным значениям, в качестве которых вначале используем стационарные
(6). Подстановка (19) в (18) с учетом стационарности (6) показывает, что
управляющий параметр 
оказывается достаточно большим,
что позволяет упростить стационарные выражения
. (20)
Вычисления
показывают, что критерий (11) выполняется для первого стационарного состояния с
превышением, а для второго при 
. Критерий (18)
выполняется для второго стационарного состояния при 
.
Таким образом, для стационарного состояния условия хаоса выполняются.
После стационарного анализа необходимо выяснить влияние начальных состояний на режимы, так как известно, что начальные условия влияют на динамику и могут привести к изменению режимов.
Чтобы
прояснить роль 
следует использовать локальные
СУ и критерии. На их основе можно выделить области начальных значений
допускающих НУ и хаос. Рассмотрим, например, основной локальный критерий (11)
. (21)
Для получения
ограничений на 
выразим 
как в стационаре
(22)
Из
выполнимости этого критерия, с учетом ограничения (4), получаем 
.
Непосредственное численное решение задачи с начальными условиями (-1,-1,-1) , а=0.25, r=4 подтвердило наличие хаотического режима.
Таким образом, использование сингулярно-динамической методики и критериев, полученных на ее основе для пока ограниченного круга задач, позволяет предсказывать неустойчивости и хаотические режимы. Применяя полученные критерии, можно управлять состояниями и динамическими режимами систем, что весьма важно в практических целях.
Литература
1. Перевозников Е.Н., Скворцов Г.Е., К теории устойчивости неравновесных систем, ЖТФ, вып.12,№ 52, 1982, с (2353-2361).
2. Перевозников Е.Н., Скворцов Г.Е., Физическая неустойчивость и качественные переходы, Materialy X miedzynarodwej naukowi-praktycznej konferencji, v30,2014, p (79-84).
3. Скворцов Г.Е., Перевозников Е.Н., Динамические качественные переходы, Materialy X miedzynarodwej naukowi-praktycznej konferencji, v31,2014,р.(82-84).
4. Скворцов Г.Е.,О закономерностях неравновесных процессов, Письма ЖТФ, т.16вып.17,1990,с.(15-17).
5. Скворцов Г.Е., Система законов природы, СПб., 2004, 116с.
6. Перевозников Е.Н., Скворцов Г.Е., Динамика возмущений и анализ устойчивости неравновесных систем, СПб.,2010, 140 с.
7. Кузнецов С.П., Динамический хаос, М.,2006, 356 с.
Поступила в редакцию 07.07.2015 г.