Исследование диэлектрической антенны вытекающей волны на подрешетках в режиме поперечного излучения

Чередниченко Виктория Федоровна,

Убогий Иван Александрович,

магистранты факультета радиотехники и электроники Воронежского государственного технического университета.

Рассматривается микроволновая антенна, апертура которой образована плоским диэлектрическим волноводом (ПДВ). ПДВ возбуждается в торец волной, вектор напряженности электрического поля (Е) которой расположен в плоскости апертуры перпендикулярно продольной оси ПДВ. На поверхности ПДВ периодически размещены проводники, регулярные в направлении вектора Е. Рассматриваемая антенна относится к дифракционным антеннам вытекающей волны (ДАВВ), обзор которых представлен в [1].

Механизм работы ДАВВ основан на известном явлении трансформации замедленной (линией передачи) поверхностной волны в вытекающую (излучаемую) волну посредством дифракционной решетки (ДР) с шагом, соизмеримым с длиной излучаемой волны l [2]. Ключевым преимуществом ДАВВ является близкое к единице отношение мощностей вытекающей и поверхностной волн. В сочетании с малым поперечным размером и надежностью, вытекающей из простоты конструкции, это обеспечило значительный интерес к ДАВВ. ДАВВ, исполненные на разных типах линий передачи, с использованием разных видов ДР и устройств возбуждения, нашли применение в системах наземной и спутниковой радиосвязи, радиолокации, радиовидения, охранных системах, в качестве эталонных антенн и др. [3, 4].

Недостатками ДАВВ является часть свойств антенных решеток с последовательным возбуждением элементов. Это и неравномерное амплитудное распределение поля по апертуре, определяющее невысокую эффективную площадь раскрыва, недостаточно малый уровень бокового излучения, характерные для неоптимизированной конструкции, и которые могут быть скорректированы лишь на основе оптимизации [5-7]. Отдельные недостатки, например, зависимость направления излучения от частоты, напротив, обостряют и обращают в преимущества [8-10]. Другой недостаток — сложность получения эффективного режима поперечного излучения (РПИ) при одностороннем возбуждении апертуры. Снижение излучательной способности в РПИ связано с проявлением дифракции Брэгга (ДБ), при которой превалирующая доля мощности поверхностной волны отражается ДР, а отраженная волна, обладающая такой же фазовой скоростью, излучается ДР в противофазе к первичной поверхностной волне. В результате обе вытекающие волны интерферируют и аннигилируют [2]. В связи с этим представляется целесообразным исследовать методы трансформации исходной геометрии апертуры ДАВВ, позволяющие ослабить или компенсировать проявление ДБ и, тем самым, обеспечить эффективный РПИ. На такую возможность указывает, например, следующее. В [11] эффекты, связан­ные с ДБ, в ДАВВ на основе нагруженной ПДВ отражательной гребенки, частично ослабляют профилированием гребенки. В [12] используют разбиение антенной решетки на подрешетки, размещаемые в узлах неравномерной сетки, что позволяет подавить интерференционные максимумы в диаграмме направленности (ДН).

Цель работы — на основе численного моделирования исследовать РПИ диэлектрической ДАВВ и показать возможность устранения ДБ.

 Для выполнения поставленной цели использована математическая модель диэлектрической ДАВВ, представленная в [13]. В ней апертура рассмотрена как двумерная (ширина неограниченна), возбуждается поверхностной волной с единственной Е-компонентой и представляет собой ПДВ (толщиной t с относительной диэлектрической проницаемостью e) на идеально проводящем основании с нанесенной на его поверхности ДР из N проводников малого радиуса (r << l) (рис. 1). Расстояния между элементами ДР, в общем случае, произвольны, в частном случае — одинаковы и равны шагу ДР (ℓ).

Обучение чтению россия

обучение чтению россия

master-class.online

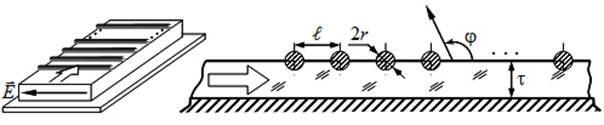
Рис. 1. Модельное представление апертуры ДАВВ.

Не вдаваясь в особенности численной модели [13], подчеркнем, что модель учитывает краевые эффекты, возникающие из-за конечного числа элементов ДР. По найденным токам в элементах ДР рассчитывается ДН в Н-плоскости — F²(j), а на ее основе — отношение мощностей вытекающей и поверхностной волн (КПД, h), коэффициенты отражения от ДР (k²_отр) и прохождения к периферии ДР (k²_пр) поверхностной волны, коэффициент использования площади (длины) апертуры (КИП, n) ДАВВ и др.

Пусть длина волны, поддерживаемой ПДВ и возбуждающей ДР, составляет в вакууме l = 7,143 мм (частота — f = 42 ГГц), ПДВ выполнен из материала с e = 9,8 толщиной t = 0,2l. Число проводников ДР N = 50 (радиуса r = 0,035λ). В [14] установлены оптимальные значения шага ДР исследуемой ДАВВ, обеспечивающие максимальные значения произведения KПД на KИП при излучении в близком к поперечному направлении. В [15] найден шаг ДР, гарантирующий наименьший уровень бокового излучения ДАВВ.

В рамках настоящего исследования установлено, что при ℓ = 0,406λ КПД апертуры с указанными выше параметрами значительно снижается (до 9,5 %), что связано с проявлением ДБ второго порядка в РПИ. Амплитудное распределение по апертуре оказывается близким к равномерному, так что n ® 1, а максимальный уровень бокового излучения составляет –13.2 дБ.

На рис. 2 показаны полученные путем моделирования зависимости КПД апертуры, коэффициентов отражения и прохождения поверхностной волны от числа элементов ДР в РПИ. Из рис. 2 следует, что коэффициент отражения падает (от 64 до 6 %) при уменьшении N от 15 до 2, однако, при этом коэффициент прохождения растет (от 14 до 78 %). КПД при N = 7 имеет максимум — h = 26,4 %, при этом k²_отр = 36,2 %. Это позволяет использовать 7-ми элементную часть апертуры как подрешетку в составе апертуры. Разбив ДР на подрешетки, содержащие по 7 элементов, следует разнести их в пределах единой ДР на расстояния, отличные от шага ДР, но обеспечивающие синфазное сложение излучаемых подрешетками полей. Поскольку каждая из подрешеток в РПИ характеризуется значительно более высоким КПД, нежели единая ДР без разнесения подрешеток, апертура с разнесением подрешеток может потенциально гарантировать высокую излучательную способность.

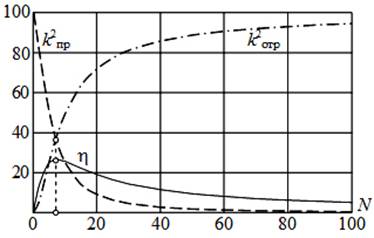
Рис. 2. Энергетические параметры апертуры ДАВВ в РПИ.

Для проверки сформулированного тезиса выполнено численное моделирование, при котором ДР из 49-ти элементов была разбита на подрешетки по 7 элементов, а расстояния между ними Dℓ_i, где i = 1...6, подбирались так, чтобы обеспечить максимум КПД апертуры при сохранении РПИ. Поскольку метод последовательного перебора при отыскании подходящих значений Dℓ_i приводит к неоправданно большим затратам времени, для поиска максимума целевой функции использован генетический алгоритм, аналогичный тому, который применен при оптимизации ДАВВ интерферометрического типа в [16] и отыскании минимаксных значений уровня бокового излучения равноамплитудной неэквидистантной антенной решетки [17]. Результаты оптимизации — расстояния между подрешетками — представлены в таблице 1, ДН — на рис. 3. Расчеты показывают, что КПД апертуры после оптимизации взаимного расположения подрешеток увеличился до 87,6 (!) %, а коэффициент отражения поверхностной волны от ДР уменьшился до 11,3 %. Это следует считать подтверждением сформулированного выше тезиса. Однако рост КПД в РПИ сопровождается снижением направленных свойств ДАВВ — КИП уменьшился до 0,51. Для улучшения ДН, видимо, необходимо использовать критерий, учитывающий КИП апертуры. Дополнительная коррекция формы ДН может быть выполнена путем подбора оптимального закона изменения по длине апертуры ширины проводников, реализованных, например, в виде лент [18].

Таблица 1.

Расстояния между подрешетками, полученные при оптимизации.

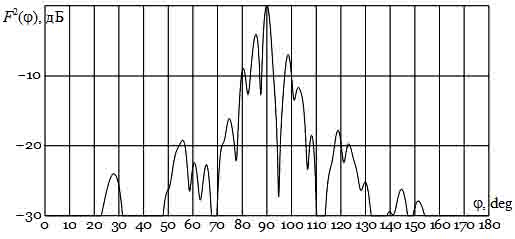
Рис. 3. ДН апертуры ДАВВ на подрешетках в РПИ после оптимизации.

Таким образом, выполнено исследование ДАВВ, параметры апертуры которой подобраны так, чтобы излучение осуществлялось строго поперечно. Получена зависимость КПД апертуры от числа элементов ДР, позволившая выбрать размер однотипных подрешеток в составе апертуры ДАВВ. Выполнена оптимизация взаимного расположения подрешеток по критерию максимума КПД в РПИ, которая подтвердила возможность устранения ДБ и значительного увеличения излучательной способности апертуры ДАВВ.

Литература

1. Останков А.В. Ретроспективный анализ возможностей, конструкций и основных характеристик дифракционных антенн вытекающей волны // Вестник Воронежского государственного технического университета. 2010. Т. 6. № 8. С. 75-81.

2. Шестопалов В.П. Физические основы миллиметровой и субмиллиметровой техники. Т. 1. Открытые структуры. Киев: Наукова думка, 1985. 216 с.

3. Евдокимов А.П. Антенны дифракционного излучения // Физические основы приборостроения. 2013. Т. 2. № 1. С. 108-124.

4. Плоская измерительная антенна СВЧ диапазона волн с электронным управлением поляризации излучения / К.Б. Меркулов, А.В. Останков, Ю.Г. Пастернак и др. // Приборы и техника эксперимента. 2003. Т. 46. № 3. С. 162-163.

5. Останков А.В. Анализ и оптимизация дифракционной антенны поверхностной волны // Антенны. 2010. № 9 (160). С. 44-53.

6. Останков А.В. Синтез излучающего гребенчатого раскрыва антенны вытекающей волны // Радиотехника. 2012. № 2. С. 38-44.

7. Останков А.В., Калинин Ю.Е., Сахаров Ю.С. Оптимизация распределительно-излучающей системы дифракционной антенны по критерию минимума угловой дисперсии в полосе частот // Вестник Воронежского государственного технического университета. 2013. Т. 9. № 6-3. С. 30-32.

8. Климов А.И. Разработка и исследование плоских дифракционных антенн СВЧ и КВЧ диапазонов с электрически управляемыми характеристиками. Воронеж: Научная книга, 2010. 118 с.

9. Останков А.В., Калинин Ю.Е. Расчет частотно-сканирующей антенны дифракционного излучения // Радиотехника. 2014. № 3. С. 83-87.

10. Останков А.В., Степанов А.Е. Методика расчёта частотно-сканирующей антенны вытекающей волны дифракционного типа // Вестник Воронежского государственного технического университета. 2012. Т. 8. № 7-1. С. 133-139.

11. Останков А.В. Дифракционная антенна вытекающей волны с нестандартной реализацией излучающего раскрыва // Вестник Воронежского государственного технического университета. 2010. Т. 6. № 8. С. 17-26.

12. Mailloux R.J. Phased Array Antenna Handbook. 2nd ed. Norwood, MA: Artech House, 2005. 496 p.

14. Калиничев В.И., Куранов Ю.В. Дифракция поверхностных волн на решетке металлических стержней и анализ диэлектрической антенны вытекаю­щей волны // Радиотехника и электроника. 1991. Т. 36. № 10. С. 1902-1909.

15. Чередниченко В.Ф. Расчет оптимального шага дифракционной решетки в составе излучающего раскрыва антенны вытекающей волны миллиметрового диапазона [Электрон. ресурс] // Современные научные исследования и инновации. 2014. № 7 (39). URL: http://web.snauka.ru/issues/2014/07/36583.

16. Чередниченко В.Ф. Оптимизация на основе математического моделирования характеристик диэлектрической антенны вытекающей волны // Современная наука: актуальные проблемы теории и практики. Серия: Естественные и технические науки. 2014. № 7-8. С. 7-11.

17. Останков А.В. Оптимизация антенны дифракционного излучения, реализованной по интерферометрической схеме // Вестник Воронежского государственного технического университета. 2010. Т. 6. № 11. С. 51-54.

18. Останков А.В., Антипов С.А., Сахаров Ю.С. Минимаксный уровень бокового излучения равноамплитудной неэквидистантной антенной решетки // Вестник Воронежского государственного технического университета. 2013. Т. 9. № 6-3. С. 10-12.

19. Останков А.В., Кирпичева И.А. Расчет параметров решетки из проводящих лент на экранированном диэлектрическом волноводе для антенны дифракционного излучения // Современная наука: актуальные проблемы теории и практики. Серия: Естественные и технические науки. 2015. № 1-2. С. 3-10.

Поступила в редакцию 26.03.2015 г.