Методика структурно-морфологического районирования на примере территории листа N-38

Мовчан Игорь Борисович,

кандидат геолого-минералогических наук, доцент,

Яковлева Александра Анатольевна,

кандидат физико-математических наук, доцент.

Санкт-Петербургский горный институт.

Постановка задачи

Выполнить прослеживание по заявленной площади элементов геоблокового строения и элементов геологической трещиноватости на основании параметрической качественной интерпретации аномальных гравитационного и магнитного полей. Реализовать элемент актуализации геологической основы на базе классификации статистического распределения значений указанных потенциальных полей.

Методика решения задачи

Картирование элементов геоблокового строения территории опирается на численный алгоритм свертки, при котором реализуется оценка границ областей неизменного амплитудно-частотного состава комплексного потенциального сигнала. Последний сформирован на основе взаимно-корреляционной функции, прямое Фурье-преобразование которой даёт кросс-спектр [1]. По отношению к кросс-спектру определяется длина волны (интервал длин волн), на который приходится максимум квадрата амплитуды кросс-спектра. Эта длина волны (интервал длин волн) определяется по аналогии с физикой волновых процессов как несущий и выносится в легенду к схеме. Интервал интегрирования в численном алгоритме свертки равен радиусу кросс-корреляции, определяемому по двум координатным осям. Резкое изменение несущей длины волны интерпретируется как шовная зона контактирующих геоблоков, каждому из которых для наглядности присваивается свой крап, также выносимый в легенду к схеме.

Прослеживание элементов геологической трещиноватости сродни так называемому линеаментному дешифрированию в аэро-космогеологии. Здесь рассматриваются гетерогенные морфоструктурные элементы условного рельефа в пространственном распределении значений потенциальных полей, выстраиваемые вдоль единых пространственных осей. По отношению к последним реализуется классификационный алгоритм, разделяющий эти оси на линейные и дуговые. Под морфоструктурными элементами понимаем цепочки аномалий, градиентные зоны, линейные аномалии, области резкой смены морфологии изолиний. Выделение градиентных зон опирается на цифровую матрицу суммы квадратов первых производных потенциального сигнала. Локализация резкой смены морфологии изолиний использует пересчет потенциального сигнала в параметр его пространственной изменчивости: среди достаточно широкого спектра подобных показателей наиболее предпочтительным оказывается параметр энтропии [2]. Таким образом, картирование линейных и дуговых осей ориентированы на три цифровые матрицы – исходного сигнала, параметра его пространственной изменчивости и модуля вектора пространственного градиента. По отношению к каждой матрице реализуется последовательность операций: локализация точек экстремумов; применение к каждой точке локальной сплайн-интерполяции для предельного сгущения цифровой матрицы; организация вращения относительно точки экстремума локального отрезка с постоянным угловым шагом в диапазоне от 0 (направление на условный север) до 180 градусов; отбор для каждой позиции вращающегося отрезка значений соответствующей цифровой матрицы, расположенных вдоль линии этого отрезка; расчет параметра изменчивости по отобранным значениям для данного азимута поворота локального отрезка; построение функционала пространственной изменчивости в зависимости от азимута поворота локального отрезка; определение оптимального азимута простирания локального отрезка на основе позиции минимального значения параметра пространственной изменчивости. Минимум пространственной изменчивости значений избранной цифровой матрицы отвечает простиранию локального отрезка вдоль оси простирания одной из указанных выше морфоструктурных особенностей обрабатываемого скалярного поля. Отклонение двух ближайших локальных отрезков по азимуту простирания более чем на 10 градусов относительно средней линейной пространственной оси означает объединение этих локальных отрезков в линейную структуру. Картирование линейных структур всегда первично, поскольку кольцевая структура часто бывает ложной: получается либо за счет маркирования зоны выклинивания структурно-вещественных комплексов, либо за счет обобщения области пересечения линейных структур разного азимута простирания. По завершению расчета все дуговые и линейные оси выносятся на одну координатную плоскость с отсеиванием пространственных осей, не проявленных во всех обрабатываемых потенциальных полях, и исключением параллельных структурных осей вплоть до наиболее выдержанной и неразрывной.

Классификационный алгоритм предполагает обработку двумерной эмпирически накопленной гистограммы распределения значений аномального гравитационного и аномального магнитного полей. В структуре этой гистограммы выделяются позиции экстремумов как центры классов, окрестность которых представляет собой статистический отклик семейства гомогенных объектов, маркируемых на исследуемой площади одним цветом [3]. Простейший случай допускает принятие в качестве центра классов максимумов двумерной гистограммы, а в качестве границы класса - брать геометрическое множество точек, отмечающих минимумы и седловые точки в структуре этой гистограммы. Значения аномального гравитационного и аномального магнитного полей, измеренных в строго заданной точке исследуемой площади и попадающие единовременно внутрь определенного класса, маркируемого строго заданным цветом, относят отмеченную точку к этому классу. Окрестность указанной точки маркируется цветом, присвоенным данному классу. Вся территория изучаемого листа разбивается на систему классов (рис.1), в границах каждого из которых исследуется соотношение участвующих в классификации потенциальных полей по их амплитуде и морфологии их карты изолиний. Цвета (крап) классов и отвечающие им характеристики полей выносятся в легенду результирующей схемы.

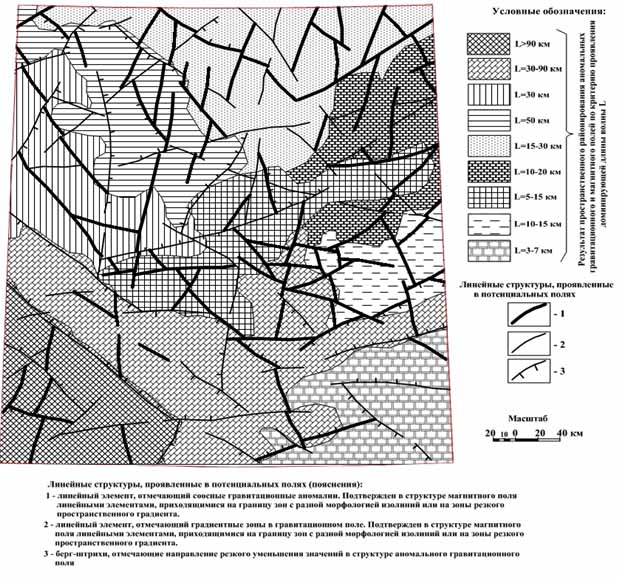
Рис. 1. Картографический результат структурно-морфологического районирования: геоблоковое строение площади листа N-38 с реконструкцией геологической трещиноватости.

Особенности конечного результата

Рассмотренные критерии качественной интерпретации пространственной структуры потенциальных полей и методы их совместной обработки относятся к линейной статистике. Термин «линейная» означает применимость её математического аппарата к экспериментальным выборкам, функция распределения которых подчиняется распределению Лапласа. Такие выборки принято называть однородными. В геологической практике однородные выборки считаются абстракциями, поэтому применение критериев и методов линейной статистики способно дать геологически значимый результат только в рамках алгоритма численной свертки, т.е. при обработке потенциального поля в условиях его разбиения на локальные и перекрывающиеся выборки.

Методика качественной интерпретации, включающая технологии районирования и прослеживания линейных и кольцевых структур, в принципе, считается универсальной по отношению к различным структурно-тектоническим обстановкам. Вместе с тем, геологическое содержание итоговых схем сильно зависит от масштаба исследований, а уровень проработки стратиграфических и тектонических контактов в итоговых схемах районирования будет определяться, с одной стороны, степенью дискретизации пространственного сигнала, и с другой стороны, степенью сложности структуры геологического пространства. В общем случае рекомендуется последовательное применение рассмотренных процедур качественной интерпретации с последующим комплексным представлением итоговых схем: прослеживание пространственных осей на фоне схемы геоблокового дробления; прослеживание пространственных осей на фоне схемы статистической классификации. Объективность конечного результата подчеркивается взаимной корреляцией этих схем.

Принципиальным элементом обработки можно назвать интерактивный характер качественной интерпретации. В случае геоблоковой схемы речь идет о варьировании размеров интервала интегрирования в алгоритме численной свертки. При прослеживании пространственных осей необходимым оказывается подбирать оптимальный размер участвующего во вращении локального отрезка, притом что его наивероятнейший размер определяется из усредненного по осям радиуса автокорреляции соответствующего потенциального сигнала. Реализация алгоритма классификации, как минимум, предполагает сужение числа классов до оптимального, как максимум – определение метода локализации классов от элементарного ранжирования эмпирически накопленной двумерной гистограммы распределения до применения нелинейной дискриминантной функции, разделяющей соседние классы в структуре данной гистограммы.

Литература

1.                  Орлов В.К. Анализ и выделение связи аномалий Буге с высотами рельефа // Диссертация на соискание степени канд.физ-мат.наук, 01.04.12, Ленинград, 1984, 149 с.

2.                  Никитин А.А. Статистические методы выделения геофизических аномалий // М., Недра, 1979, 280 с.

3.                  Богоутдинов Ш.Р. Алгоритмы нечеткой логики при интерпретации геолого-геофизических данных // Диссертация на соискание степени канд.физ.-мат.наук, 25.00.10, М., 2007, 139 с.

Поступила в редакцию 21.04.2016 г.