Применение комплекса аналитических продолжений потенциальных полей на примере участка сейсмического профиля m-714 листа N-38

НА ГЛАВНУЮ

Мовчан Игорь Борисович,

кандидат геолого-минералогических наук, доцент,

Яковлева Александра Анатольевна,

кандидат физико-математических наук, доцент.

Санкт-Петербургский горный институт.

Постановка задачи

Выполнить количественную интерпретацию указанных потенциальных полей с построением семейства разной специализации параметрических разрезов, пространственная коррелируемость которых допускает построение взаимоувязанного синтетического разреза.

Методика решения задачи

Интерпретация аномального гравитационного поля предполагает несколько математически независимых методов, включающих в рамках данного пересчета метод волновой аппроксимации (рис.1,а) [1], сопряженный с ним метод расчета нормированного плотностного параметра (рис.1,б) [2], а также аналитическое продолжение по Страхову с выметанием сингулярностей (рис.1,в,г) [3]. Метод волновых аппроксимаций ориентирован на разложение пространственного сигнала в систему стоячих волн. Под ними понимаются составляющие этого сигнала, укладывающиеся в узкий интервал пространственного периода, обладающие «узлами» на границе выборки – нулевой амплитудой, характеризующиеся на отдельных пространственных интервалах целочисленными значениями пространственного периода. В основе такого анализа заложено вейфлет-преобразование. Каждая из составляющих относится к детерминированному интервалу глубин на основе соотношения между доминирующей длиной волны (пространственного периода) и предельной глубины залегания аномалеобразующей геологической неоднородности [4]. В общем случае имеет место закон дисперсии волн [5], согласно которому при постоянной частоте источника волн связь между длиной волны и предельной глубиной её проявления описывается логистичекой функцией. Значения узкополосной составляющей пространственного сигнала относится к вычисленной предельной глубине залегания аномалеобразующих неоднородностей. Конечный результат расчета включает цифровую матрицу, задающую распределение исходного пространственного сигнала по системе волновых функций в плоскости разреза. Приведение его в интерпретируемую форму опирается, с одной стороны, на метод ГРАД (Справочник по гравиразведке, 1985) и, с другой стороны, на расчет нормированного плотностного параметра:

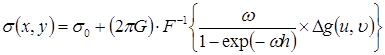где - априори задаваемое фоновое значение плотности в разрезе, - гравитационная постоянная, - символ обратного Фурье-преобразования, и - пространственные частоты, выделяемые, соответственно, вдоль осей «x» и «y», , - глубина отнесения пересчета. Применение метода ГРАД в комплексе с системой подобранных спектральных фильтров представить параметрический разрез в полутоновой структурной форме, допускающей локализации поверхностей раздела по аналогии с временными сейсмическим и георадарным разрезами (Апробация по сейсмическому профилю AP-I). Аналитическое продолжение с выметанием сингулярностей представляет собой пересчет потенциального сигнала в нижнее полупространства с использованием разложений, подобных разложениям в ряд по классической методике Берёзкина. С ростом глубины на локальном интервале профиля по мере приближения к аномалеобразующей геологической неоднородности (точке сингулярности) потенциальный сигнал начинает испытывать в ее окрестности выраженные осцилляции. Последние проявляются в росте амплитуды спектральных гармоник в узком диапазоне длин волн, на который следует накладывать подавляющую апертуру. После этого потенциальный сигнал можно пересчитывать ниже глубины залегания точки сингулярности. Как и в случае с вычислением нормированного плотностного параметра, результат аналитического продолжения представлен в форме плоскости параметрического разреза, в котором изолиниями задано распределение значений скалярного поля.

Интерпретация аномального магнитного поля в данном случае ограничивалась аналитическим продолжением с выметанием сингулярностей, для верификации особенностей которого применялся способ аппроксимирующих дробей. Его основу составляют семейства известных аналитических решений прямой задачи теории потенциала, определяющих функциональную взаимосвязь между значениями измеренного на земной поверхности потенциального сигнала и физико-геометрическими характеристиками скрытой геологической неоднородности. Аппроксимируя последние простейшими телами (сфера, призма и проч.), возможно указанные функциональные зависимости преобразовать в подобие конечного ряда, где левая часть определяется фактическими значениями потенциального сигнала в конкретных точках профиля, а правая часть, наряду с координатами этих точек, содержит физические и геометрические характеристики тела. Данный подход применяем в комплексе с численной процедурой свертки, в которой оптимальный размер интервала интегрирования определяем на основе радиуса автокорреляции пространственного сигнала. Для каждой позиции интервала интегрирования решаем систему линейных уравнений, образованных на основе указанного выше конечного ряда. Результат решения имеет форму распределения особых точек в плоскости параметрического разреза, пространственно совпадающих с характерной точкой тела простейшей геометрии, аппроксимирующего геологическую неоднородность.

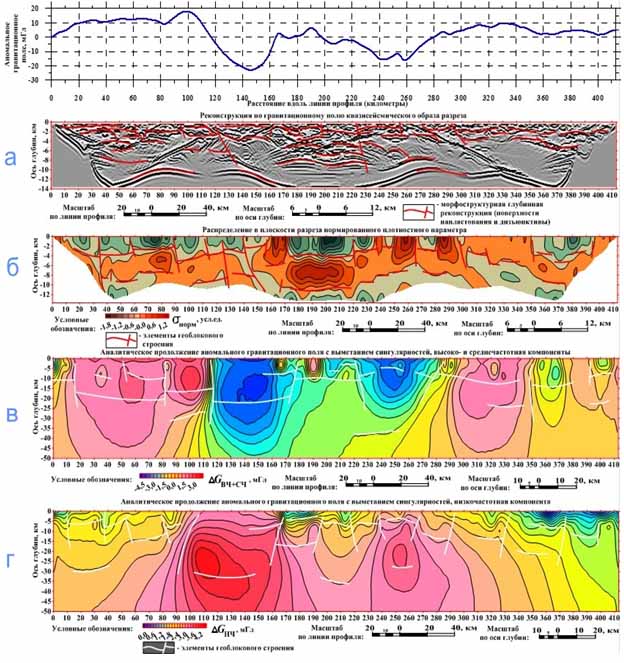
Рис. 1. Пример применения комплекса аналитических продолжений по участку профиля m-714: а. – результат квазиволновых аппроксимаций; б. - распределение в плоскости разреза параметра эффективной плотности; в. г. – образы потенциального поля в плоскости разреза. На фоне формальных параметров нанесены элементы разрывной тектоники и стратификации геологической среды.

Каждая точка характеризуется усредненной физической характеристикой (нормированным плотностным параметром или модулем вектора магнитного момента). В плоскости параметрического разреза на результат аналитического продолжения накладывается вычисленное семейство точек, в котором усредненная физическая характеристика проявлена как нормирование размеров этих точек.

В случае аномального гравитационного поля отчетная графика содержит четыре параметрических разреза (рис.1):

1. Реконструкция по гравитационному полю квазисейсмического образа. Разрез имеет полутоновую форму, отражающую элементы стратификации примыкающей к плоскости разреза геологической среды, позицию отдельных контактных поверхностей, син- и антиформы, возможные глубинные разломы и сутуры.

2. Реконструкция распределения в плоскости разреза нормированного плотностного параметра. Разрез представлен в форме схемы изолиний скалярного поля соответствующего содержания, отражающего элементы стратификации примыкающей к плоскости разреза геологической среды, а также элементы геоблокового строения.

3. Два способа аналитического продолжения гравитационного поля:

3.1. Верхний разрез построен на основе аппроксимации четными функциями. Аномалеобразующие источники локализованы в окрестности точек экстремума. В мелких масштабах этот тип аналитического продолжения позволяет определить предельные глубины залегания неоднородностей, ответственных за средне- и высокочастотную компоненты пространственного потенциального сигнала;

3.2. Нижний разрез построен на основе аппроксимации нечетными функциями. Аномалеобразующие источники локализованы в окрестности точек экстремума. В мелких масштабах данный способ аналитического продолжения допускает, во-первых, прогнозирование морфологии контактной поверхности «фундамент-осадочный чехол», во-вторых, определение глубины залегания неоднородностей, ответственных за низкочастотную составляющую пространственного потенциального сигнала.

В случае аномального магнитного поля расчеты ограничивались компоновкой двух параметрических разрезов, содержание которых описано в п.3 предыдущего абзаца. На каждый из этих разрезов наложено семейство особых точек, вычисленных методом аппроксимационных дробей.

Замечание 1. Отсутствие выраженного замыкания изолиний скалярных полей, определенных в плоскости параметрических разрезов, с выходом этих изолиний на глубины, превышающие предельные глубины аналитических продолжений, не означает прогноз аномалеобразующих геологических неоднородностей на произвольно больших глубинах. Собственно неоднородности, согласно численному алгоритму и физическим основам методов пересчета, локализованы в окрестности точек экстремума скалярного поля. Продолжение изолиний этого поля далеко в сторону (по глубине и по латерали) от точек экстремума обусловлено, во-первых, априорной гипотезой о непрерывном характере исходного потенциального поля за пределами аномалеобразующего источника, во-вторых, применением набора сглаживающих спектральных окон при «выметании сингулярностей».

Замечание 2. Использование при количественной интерпретации спектральных преобразований заставляет:

2.1. исключать из рассмотрения объекты, отраженные в плоскости параметрического разреза в непосредственной близи (4 точки отсчета, т.е. 2 км для гравитационного поля и 1 км – для магнитного) от концов профиля;

2.2 применять в пределах всей выборки куполообразгую спектральную функцию Хэннига для исключения паразитных осцилляций в структуре параметрического разреза.

Замечание 3. В структуре параметрических разрезов достоверными можно считать латеральную позицию выявленных неоднородностей, их взаимное пространственное соотношение, морфологию протяженных по латерали и/или глубине особенностей, относимых к контактным поверхностям или иным пространственным элементам аппроксимирующих тел. Достоверность глубины, равно как величины усредненного физического параметра, характеризующих локализованную геологическую неоднородность, сильно зависит от априорной информации и применяемых моделей в решении обратной задачи теории потенциала.

Литература

1. Прикладные аспекты теории диссипативного структурирования неравновесной геологической среды / В кн. Петров О.В. Диссипативные структуры Земли как проявление фундаментальных волновых свойств материи. СПб, ВСЕГЕИ, 2007, С. 202-268.

2. Gupta V.K., Grant F.S. Mineral-exploration aspects of gravity and aeromagnetic surveys in the Sudbury – Cobalt area, Ontario // The utility of regional gravity and magnetic anomaly maps, Tulsa, USA, 1985, pp. 3932-412

3. Арсанукаев З.З. Аналитическое продолжение заданных значений гравитационного поля в дискретной постановке через источники в двумерном случае // Вестник Краунц, №1, вып.№13, 2009, С.47-57.

4. Черников А.Г., Либина Н.В., Матушкин М.Б. Способ выявления внутренних неоднородностей Земли / Заявка на изобретение 2004138868/28, 30.12.2004.

5. Петров О.В., Мовчан И.Б. Диссипативное структурирование земной коры и мантии как отражение волновых процессов // Журн. Региональная геология и металлогения, №12, 2002, С.57-66.

Поступила в редакцию 21.04.2016 г.