Численное решение дифференциальных уравнений методом Эверхарта
Хикматова Рано Артиковна,
старший преподаватель,
Садуллаева Мавжуда Зиёдуллаевна,
ассистент.
Ташкентский автомобильно-дорожный институт, Республика Узбекистан.
При решении многих прикладных задач (например, в небесной механике) явные многошаговые методы Коуэлла не позволяли существенно расширить интервал интегрирования. Разработанный Эверхартом метод численного интегрирования обыкновенных дифференциальных уравнений позволяет снять это ограничение, что особенно важно при решении задач динамики.
Метод Эверхарта является одной из разновидностей методов Рунге-Кутты. Он относится к числу неявных одношаговых методов, что обеспечивает его сходимость и устойчивость. Основным достоинством одношаговых методов является то обстоятельство, что для них разработаны надежные оценки локальной погрешности дискретизации. Кроме того, метод Эверхарта показал себя как самый эффективный по точности и быстродействию в эксперименте по исследованию алгоритмов и программ численного прогнозирования движения небесных тел.
Вследствие того, что повышение порядка аппроксимирующей формулы в большинстве случаев улучшает основные свойства методов, разработка группы методов Эверхарта более высокого порядка, по сравнению с существующими, является актуальной задачей с целью создания более точного и эффективного алгоритма численного интегрирования [1].
Алгоритм и программа численного интегрирования методом Эверхарта ранее были разработаны до 27 порядка, однако использование этих алгоритмов свыше 19-го порядка не приводило к повышению точности вычислений.
Рассмотрим основную идею построения метода Эверхарта на примере решения уравнения вида
(1)
Представим правую часть в виде временного ряда
(2)
Интегрируя это, получим выражения для определения координат и скоростей:
(3)
(4)
Полиномы (3) и
(4) не являются рядами Тейлора, а коэффициенты 
вычисляются из условия наилучшего приближения 
и 
с помощью конечных разложений (3) и (4). Для связи А-значений
с F- значениями воспользуемся вспомогательным выражением
(5)
Уравнение (5)
усечено по времени 
. В каждый фиксированный момент времени 
имеем
(6)
……………………………….
Принимая 
найдем 
через разделенные разности:
(7)
……………………………………………………….
Приравнивая
коэффициенты при одинаковых степенях t в уравнениях (2) и (5), выразим
коэффициенты через :
(8)
…………………………………
Коэффициенты
определяются из следующих рекуррентных соотношений:
(9)
для алгоритма интегрирования пятого порядка
(10)
где 
являются корнями кубического уравнения
+(
)t+
(11)
Таким образом,
нахождение решения уравнения сводится к нахождению узлов разбиения шага h.
Вопрос нахождения узлов разбиения шага h=[0, T] рассмотрим на примере алгоритма интегрирования пятого порядка.
В начальный
момент времени 
известны 
. Значения x в моменты времени определяются с помощью трех предсказывающих
уравнений:
(12)
(13)
(14)
И двух исправляющих уравнений для нахождения положения и скорости на конце шага h :
(15)
(16)
Эта схема является неявной, так как коэффициенты, стоящие в квадратных скобках (12) – (14), неизвестны при первой итерации [2, 3].
Уравнение (12) –
(16) обеспечивают пятый порядок точности относительно t . Можно увеличить
порядок точности в вычислении x и 
до седьмого порядка путем специального
выбора подшагов . С этой целью увеличим количество разбиений интервала
интегрирования, добавив два дополнительных времени 
. Затем вычислим для 
и 
значения 
и 
, а также новые значения 
, 
и 
, 
Из уравнения
(15) можно найти поправки 
, улучшающие значения координат:
(17)
Выражая в
уравнении (9) 
через 
, а также полагая
, 
и 
(18)
Выражение (17) может быть записано в виде
Значение в последнем выражении можно обратить в ноль при
выполнении следующих условий:
(19)
Проводя подобные
рассуждения для скорости, приравнивая к нулю 
, получим третье условие для определения 
, 
. тогда соответствующие данным разбиением коэффициенты
будут определяться из системы алгебраических
уравнений
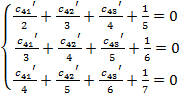(20)
Из решения этой системы
(21)
следует, что
значения величин 
являются корнями следующего полинома третьей
степени
(22)
которые имеют следующие значения:
= 0.212340538239…,
= 0.590533135559…, (23)
= 0.91141240488…
Использование
этих узлов позволяет получить решение уравнения с точностью до седьмого порядка для обеих компонент
x и 
Однако при
применении метода Эверхарта, к решению уравнений движения небесных объектов,
увеличение порядка метода не приводило к повышению точности и эффективности
вычислений. Показано, что главная причина заключалась в способе нахождения
значений 
.
Заключение
Рассмотрев различные разностные методы решения обыкновенных дифференциальных уравнений, как универсальные (методы тейлоровских разложений, Рунге-Кутте, Адамса-Бэшфорта, Адамса-Мультона), так и специализированные (Эверхарта, Коуэлла), пришли к следующим выводам.
Сравнение универсальных методов можно проводить на основе нескольких принципов: а) точности; б) надежности; в) непосредственных затрат и г) полных затрат.
Специализированный метод Эверхарта эффективно использовать при решении уравнений движения в задачах небесной механики.
Литература
1. Бахвалов Н. С. Численные методы. Т. 1. - М.: Бином.ЛЗ, 2003.– 632 с.
2. Бордовицина Т.В. Современные численные методы в задачах небесной механики. - М.: Наука, 1984. – 136 с.
3. Мысовских И.П. Лекции по методам вычислений. СПБ.: СП6ГУ, 1998. – 472 с.
4. Самарский А. А., Гулин А. В. Численные методы. М.: Наука, 1989.
Поступила в редакцию 14.03.2016 г.