Методы решения системы линейных уравнений

Хушруд Бакиев,

преподаватель кафедры методики дошкольного и начального образования Каршинского государственного университета, Узбекистан.

Чизиқли тенгламалар системасини ечиш усуллари

Хушруд Боқиев,

Қарши давлат университети “Мактабгача ва бошланғич таълим методикаси” кафедраси ўқитувчиси.

Маълумки, ўрта умумтаълим мактаблар, лицей ва академик лицейлар ҳамда касб-ҳунар коллежларининг математика дарсларида чизиқли тенгламалар системалари (номаълумлар сони тенгламалар сонига тенг бўлган ҳоллар) ечилиши кўрсатилган. Лекин номаълумлар сони билан тенгламалар сони бир-бирига тенг эмас ҳоллари кўрилмаган. n та номаълумли m та чизиқли тенгламалар системаси қўйидаги кўринишга эга бўлади:

а₁₁х₁+а₁₂х₂+а₁₃х₃+…+а_1jx_j+…+a_1nx_n=b₁

a₂₁x₁+a₂₂x₂+a₂₃x₃+…+a_2jx_j+…+a_2nx_n=b₂                                                                                    (1)

a_i1x₁+a_i2x₂+a_i3x₃+…+a_ijx_j+… + a_inx_n=b_i

a_m1x₁+a_m2x₂+a_m3x₃+…+a_mjx_j+…+a_mnx_n=b_m

бунда,  ихтиёрий ҳақиқий сонлар бўлиб, номаълумлар олдидаги коэффициентлар дейилади. b_i лар эса озод ҳадлар деб юритилади.
Бунда х_1.х₂,…,х_n - лар номаълумлардир.

(1) системани қисқача: 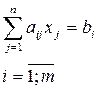                                                                 (2)

Агар х₁=к₁; х₂=к₂,…,х_n=к_n сонларни (1) системага қўйганда, системадаги ҳар бир тенгламани айниятга айлантирса, у ҳолда бу сонлар системаси тенгламалар системасининг ечими дейилади.

Агар (1) система ҳеч бўлмаса битта ечимга эга бўлса, бу система биргалашган система дейилади. Акс ҳолда, биргалашмаган система дейилади.

Агар биргаликда бўлган система ягона ечимга эга бўлса, у ҳолда бундай система аниқ система дейилади.

Агар биттадан ортиқ ечимга эга бўлса, бундай система аниқ бўлмаган система дейилади. (1) тенгламалар системасини:

;            ;

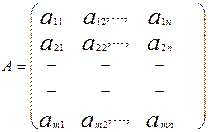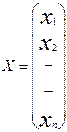Кўринишда белгилаб олсак, ушбу системани  (3) кўринишдаги матрицали тенглама шаклида ифодалаш мумкин.

(3) тенглама матрицали тенглама деб юритилади.

Фараз қилайлик, (1) системада номаълумлар сони тенгламалар сонига тенг бўлсин, унда бўлади.

У ҳолда, А матрица квадрат матрица бўлади.

Квадрат матрицанинг дитерминанти системанинг асосий дитерминанти дейилади. Агар уни D билан белгиласак

Агар D¹0 бўлса, А квадрат матрицага тескари А^-1 матрица мавжуд бўлади.

 (3) тенгламани чапдан А^{-1 га кўпайтирсак, қуйидагига эга бўламиз, яъни:}

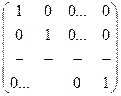А^-1×А Х=A^-1×B                         A^-1×A=E=

(A^-1×A) X=A^-1×B

Умумий ечим: Х=A^-1×B (4) га тенг бўлади.

 (1) тенгламалар системасини Крамер формуласи ёрдамида ечиш мумкин. Бунда бўлиши шарт. Агар асосий дитерминант  бўлса,
(1) система Крамер формуласи ёрдамида ечимга келади.

                                                                                                 (5)

(5) формула Крамер формуласи дейилади.

мавжудлигини эътиборга олиб, (4) формулани қўйидагича ёзиш мумкин:

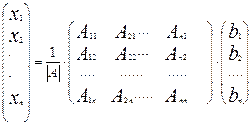 ёки

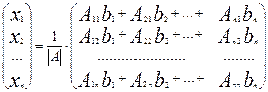                                                              (6).

Бу тенгликдан ихтиёрий j учун Крамер формуласи ни ҳосил қиламиз. Яъни:

                                                          (7)

(1) системани Гаусс усули билан ҳам ечиш мумкин. Гаусс усулининг асосий ғояси номаълумларни белгиланган қоидалар бўйича кетма-кет йўқотиш усулидан иборат. Асосий матрицада элементар алмаштиришлар ёрдамида матрицани диагонал кўринишга келтирганимизда, натижада (1) тенгламалар системасига тенг кучли тенгламалар системаси ҳосил қилинади. Ундан пастдан юқорига қараб номаълумлар кетма-кет топилади.

 (1) тенгламалар системасидан қуйидаги кенгайтирилган матрицани қараймиз.

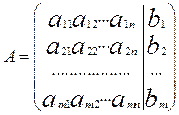
Бу матрица (1) системанинг коэффициентларидан тузилган кўпайтирилган матрица.

(1) системада элементар алмаштиришлар бажаришга нисбатан, кенгайтирилган матрицада элементар алмаштиришлар қулайроқ ҳисобланади. Маълумки, матрица ранги унинг сатр ва устунларида мавжуд бўлган чизиқли эркли векторларнинг максимал сонига айтилади.

Кронкер-Копелла теоремаси ёрдамида ҳам (1) кўринишидаги чизиқли тенгламалар системасини ечиш мумкин.

(1) тенгламалар системаси ечимга эга бўлиши учун, кенгайтирилган матрица ранги билан асосий матрица ранги бир-бирига тенг бўлиши зарур ва етарли. Бунда асосий ва кенгайтирилган матрица ранги системадаги номаълумлар сонига тенг бўлса, у ягона ечимга эга бўлади. Агар асосий ва кенгайтирилган матрица ранги номаълумлар сонидан кичик бўлса, (n-r) та номаълум ва тенгламалар устида белгиланган тартиб бўйича ечимлар топилади. Бунда озод ўзгарувчи ҳосил бўлиб, унга ихтиёрий қийматлар бериб, унга боғлиқ бўлган қолган ўзгарувчилар топилади.

Адабиётлар

1.                  А.И.Мальцев “Основы линейной алгебры” Москвa, 1978 .

2.                  А.Г.Курош. “Олий алгебра курси” Тошкент. ўқитувчи.1976.русчадан 10-нашр таржимаси.

Поступила в редакцию 29.06.2016 г.