Исследование теплообмена в канале с оребренной поверхностью методом численного моделирования
кандидат технических наук,
Подлипнова Ксения Евгеньевна,
магистрант.
Самарский государственный технический университет.
Проведено численное исследование движения потока воздуха в канале с оребренной поверхностью. Решение получено для ламинарного режима в стационарной постановке. Получена зависимость критерия Нуссельта и скорости движения теплоносителя для различных профилей оребрения. Определена оптимальная форма профиля оребрения для плоскопараллельных каналов в диапазоне критериев Рейнольдса Re = 2000÷12000.
Ключевые слова: оребренная поверхность, теплообмен, численное моделирование, воздушный калорифер, ламинарный режим.
Воздушные теплообменные аппараты (калориферы, фанкойлы и пр.) [1-3] получили широкое распространение благодаря надежности и доступности используемых теплоносителей. Они применяются в различных отраслях в том числе в системах теплоснабжения и вентиляции, в нефтегазовом хозяйстве и энергетике.
В данной работе рассмотрен пластинчато-ребристый теплообменник [4] с различной формой ребер. Определение оптимальной формы оребрения проводилось методом численного моделирования в программном пакете Code_Saturne [5]. Была использована численная модель, адекватность которой была подтверждена для случая поперечного обтекания пучка нагретых труб [6].
Для упрощения и сокращения времени расчета [7] за расчетную область был взят симметричный участок теплообменника (рис. 1) длиной L= 0,1029 м; высотой K= 0,0165 м; радиус закругления ребер R= 0,0159 м и различной высотой ребер H= 0,0159 м (рис.1 а); Н= 0,0053 м (рис.1 б); Н= 0,00265 м (рис.1 в).
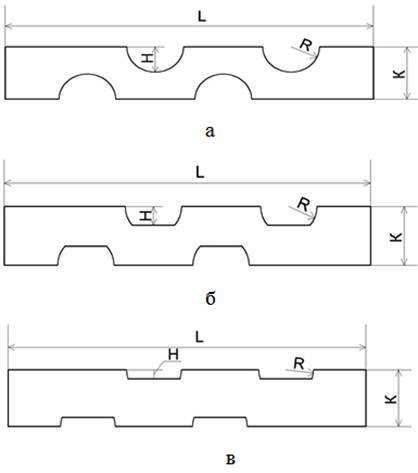
Рис. 1. Расчетная область.
Исходя из геометрии расчетной области, была построена расчетная сетка, состоящая из 15 тыс. призматических ячеек, максимальный размер ячеек 0,005 м (рис. 2). Вдоль поверхностей теплообмена построены пристеночные призматические слои [8] ∆у = 0.00138 м; количество слоев 10; коэффициент растяжения 1.2.
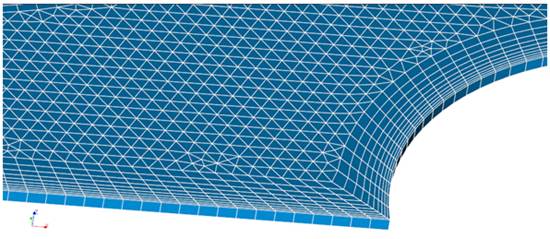
Рис. 2. Фрагмент расчетной сетки.
Расчет проводился при постоянных
параметрах воздуха при начальной температуре Т0 = 20 0С
и давлении p = 101325 Па, расчет был проведен для шести различных скоростей на
входе в теплообменник: ![]()
Задача решена в стационарной постановке
и без применения модели турбулентности, так как в экспериментальной установке
наблюдался ламинарный режим течения [9]. Уравнение неразрывности решалось по
полу-неявному методу (SIMPLEC) [10]. Максимальное количество итераций составило
2000, базовая точность решателя не превышала![]() . Для всех параметров проводилась
дискретизация второго порядка (Centered). В данном расчете не использовалась
релаксация шаговых отклонений.
. Для всех параметров проводилась
дискретизация второго порядка (Centered). В данном расчете не использовалась
релаксация шаговых отклонений.
Решение получено для 2 с эксперимента с фиксированным шагом 0.001 с. Результатом моделирования является зависимость числа Нуссельта от числа Рейнольдса (рис. 3).
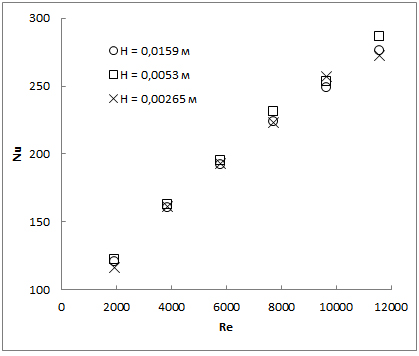
Рис. 3. Зависимость теплоотдачи от скорости потока.
Полученная зависимость показывает определенный предел роста эффективности теплоотдачи (Nu) по мере увеличения высоты ребер в рассматриваемом диапазоне чисел Рейнольдса. Для рассматриваемого случая наибольшая теплоотдача наблюдается для ребер с высотой Н = 0,0053 м.
Литература
1. Берман С. С. Теплообменные аппараты и конденсационные устройства турбоустановок. – Рипол Классик, 2013.
2. Ефимов А. В., Гончаренко А. Л., Гончаренко А. В. Система глубокой утилизации теплоты газов, уходящих из котельных агрегатов. – 2013.
3. Никульшин Р. К., Морозюк Л. И., Соколовская В. В. Анализ характеристик кожухотрубного конденсатора с целью энергосбережения // Холодильна техніка та технологія. – 2014. – №. 1. – С. 37-43.
4. Васильев В. Я. Рациональная интенсификация конвективного теплообмена рассечением длинных гладких каналов // Вестник Московского авиационного института. – 2010. – Т. 17. – №. 3. – С. 14-18.
5. Code_Saturne. URL: http://code-saturne.org/cms/ (Дата обращения 07.01.2017).
6. Подлипнова К.Е., Никитин М.Н. Численное исследование теплообмена с оберенной поверхностью// Труды Академэнерго, 2016, №4. - С. 42-49. [в печати]
7. Волков К. Н. Балансировка нагрузки процессоров при решении краевых задач механики жидкости и газа сеточными методами // Вычислительные методы и программирование. – 2012. – Т. 13. – №. 1. – С. 107-129.
8. Лашкин С. В. и др. Моделирование течений вязкой несжимаемой жидкости разделенным и совмещенным алгоритмом типа SIMPLE // Математическое моделирование. – 2016. – Т. 28. – №. 6. – С. 64-76.
9. Прандтль Л., Титьенс О. Гидро-и аэромеханика. – Рипол Классик, 2013. – Т. 2.
10. Козелков А. С. и др. Реализация метода расчета вязкой несжимаемой жидкости с использованием многосеточного метода на основе алгоритма SIMPLE в пакете программ ЛОГОС // Журнал ВАНТ. Сер. Математическое моделирование физических процессов. – 2013. – №. 4. – С. 44-56.
Поступила в редакцию 11.01.2017 г.