Оптимизация раскроя материалов в процессе их резки с помощью лазерных технологических установок

 

Костромин Михаил Анатольевич,

докторант Московского технологического университета.

 

Промышленная обработка материалов стала одной из областей наиболее широкого использования лазеров. В настоящее время лазер успешно выполняет целый ряд технологических операций и, прежде всего таких, как резка, сварка, сверление отверстий, термическая обработка поверхности, скрайбирование, маркировка, гравировка и т. п., а в ряде случаев обеспечивает преимущества по сравнению с другими видами обработки.

Раскрой материалов является одной из наиболее важных проблем. Задачу раскроя материала математически можно сформулировать как задачу линейного программирования [1].

 Пусть требуется получить комплект из n видов раскроя каждого вида в количестве  пусть - число -х видов раскроя, получающихся при раскрое одной единицы материала по способу с номером  c_i - ценность единицы материала, используемой в данном раскрое.

Обозначим через  употребительность (на один комплект)  - го раскроя. Если допустить, что все раскрои  перечислены, то задача составления плана раскроя заключается в нахождении неизвестных , удовлетворяющих требованиям:

                                                                                                          (1)

 

                                                                                               (2)

 

                                                                                                     (3)

 

В качестве метода решения задачи (1) - (3) был предложен метод разрешающих множителей [2], основанный на использовании шкалы индексов.

Известен и другой метод решения задачи линейного программирования - симплекс-метод, который по существу сходен с методом разрешающих множителей. Существуют также различные модификации указанных методов [1].

Указанные выше методы остаются основными для решения задачи раскроя на производстве и в настоящее время.

Основным недостатком этих методов является их громоздкость в связи с необходимостью генерации всего множества допустимых вариантов для получения оптимального решения.

Известны также алгоритмы использования метода дихотомии для решения широкого класса комбинаторных и оптимальных задач.

В работах [3, 4] приведены алгоритмы и программы, позволяющие решать задачу линейного раскроя на базе использования линейного программирования.

Задача линейного раскроя может быть отнесена к задачам линейного программирования с неявно заданной матрицей ограничений и для генерации столбцов, вводимых в базис.

Для решения таких задач известны различные методы, основанные на идеях динамического программирования [5].

К наиболее известным методам, в основу которых они легли, относятся:

-                   сеточный метод;

-                   метод склейки;

-                   метод северо-восточного угла;

-                   метод юго-восточного угла.

Возможность решения общей задачи раскроя без составления всех допустимых вариантов с помощью методов динамического программирования показана в [5].

Решение заключается в том, что после каждого шага симплекс-метода для выяснения способа улучшения раскроя решается небольшая вспомогательная задача и для ее решения применяются методы динамического программирования.

В качестве одного из методов решения данной задачи является алгоритм, основанный на использовании идеи построения всех возможных сочетаний.

Также известен метод последовательного улучшения оценок, основанный на применении экономической интерпретации «объективно обусловленных оценок», когда вместо решения прямой задачи решается двойственная задача линейного программирования.

Пусть заданы размеры необходимых видов раскроя  и их стоимости , размеры исходного материала  и количество  исходного материала каждого вида, необходимое для изготовления одного комплекта. Требуется найти способы раскроя и определить интенсивности их применения, обеспечивающие наиболее экономное расходование исходного материала.

Предположим сначала, что известны все возможные способы раскроя единицы материала. При этом -й способ раскроя -го вида материала характеризуется вектором

где  - количество исходного материала- го вида, получаемых из - го вида материала при - ом способе его раскроя.

Если обозначить через  - количество материала - го вида, раскраиваемых - ом способом, то интересующий нас вопрос сводится к следующей задаче.

Заданы неотрицательные числа:

Найти числа  из условий:

                                                                         (4)

                                                                              (5)

 

 .                                                                                                 (6)

 

Вектор  называется допустимым, если он удовлетворяет условиям (4) и (5), и оптимальным, если он удовлетворяет также условию (6).

Эта задача может быть решена каким-либо методом линейного программирования, например, методом последовательного улучшения допустимого вектора [6].

Показано, что для оптимальности допустимого вектора

необходимо и достаточно, чтобы существовали числа

,

удовлетворяющие следующим условиям:

                                                                                               (7)

                                                                  (8)

 

                                                                                            (9)

 

                                                                                               (10)

 

Числа имеют смысл оценок соответствующих ограничений рассматриваемой задачи.

При реализации метода последовательного улучшения допустимого вектора на каждом шаге имеется допустимый вектор  такой, что соответствующая ему система (9) - (10) содержит n уравнений и матрица В этой системы является не особенной.

Поэтому из системы (9) - (10) однозначно определяются числа  которые являются решением задачи.

На основе использования метода ветвей и границ предложены эффективные процедуры отсечения бесперспективных вариантов. Это позволило получить решения для задачи с большим количеством исходных данных (порядка 400) за приемлемое время [7].

Альтернативой точным методам могут служить дискретные аналоги градиентных алгоритмов. Они позволяют быстро и с высокой точностью решать задачи большой размерности.

Точные комбинаторно-геометрические методы имеют высокую трудоемкость в решении таких задач и поэтому, как правило, заменяются приближенными эвристическими алгоритмами [8].

Такие алгоритмы, в большинстве случаев, просто имитируют действия технолога и представляют собой некоторый набор правил конструирования наиболее экономичных карт раскроя.

Основным недостатком эвристических алгоритмов является случайность получаемого решения и сложность оценки эффективности полученного решения.

В условиях единичного производства модели раскроя значительно разнятся с моделями раскроя в условиях массового производства, и принципиально отличаются от последних требованием целочисленности переменных.

Особенностью задач целочисленного программирования является разрыв «двойственности», то есть несовпадение целевых функций для прямой и обратной задачи математического программирования, что не позволяет использовать столь эффективный для задач линейного программирования аппарат двойственности.

Основу алгоритмов решения целочисленных задач линейного программирования составляют всевозможные приемы улучшения перебора вариантов.

Наиболее распространенным точным методом решения указанной задачи является метод ветвей и границ, когда сначала определяются нижняя и верхняя границы функции цели, а затем они последовательно уточняются.

Несмотря на эффективность метода ветвей и границ, при увеличении количества переменных алгоритмы, построенные на этом методе, имеют тенденцию к перерождению в полный перебор, что недопустимо в условиях реального производства.

Для построения и анализа алгоритмов отсечения достаточно продуктивной оказалась идея введения меры эффективности отсечений с помощью -разбиения множеств конечномерного пространства.

На ее основе получен ряд теоретических результатов, в частности, выделен класс регулярных отсечений, обеспечивающий конечность алгоритмов, построены верхние и нижние оценки числа итераций.

Для решения задачи целочисленного раскроя существует множество простых приближенных алгоритмов.

Однако, как показал проведенный анализ - результаты использования подобных алгоритмов далеки от оптимальных.

В связи с развитием дискретной математики широкое развитие получили алгоритмы на графах и сетях [9].

Как было отмечено выше, задача раскроя относится к классу NP-полных.

Большинство алгоритмов решения NP - полных или трудно решаемых задач на графах строится на основе поиска, использующего дерево решений.

Чаще всего поиск реализуется с помощью процедуры перебора с возвратом.

Основной принцип такой процедуры состоит в разбиении начальной задачи Р₀ на некоторое число подзадач Р_1,Р₂, ..., Р_к, в целом представляющих задачу Р₀, с последующей попыткой разрешить каждую из этих подзадач.

Подзадачи, на которые разбивается исходная задача, должны быть проще ее (либо они имеют меньший размер, либо обладают более простой структурой).

Каждая подзадача может быть еще неразрешима и, в свою очередь, порождает подзадачи Р_п, .., Р_к.

 Рекурсия действует до тех пор, пока не будет получена простая подзадача, решение которой не представляет особого труда.

Построение дерева решений для нахождения результата используют метод ветвей и границ, венгерский метод, а также метод замещений, который будет рассмотрен далее более подробно.

Имеется множество исходного материала с размерами , где  и задано множество исходного материала с размерами , где  при этом длина  не может превышать максимальной длины  т.е.

 Заготовки получают путем раскроя исходного материала.

 Требуется минимизировать отход материалов, то есть максимизировать коэффициент использования материала, который равен отношению суммарной величины затраченного исходного материала к сумме величин полученного материала.

 При мелкосерийном и единичном производстве задача раскроя исходного материала требует решения задачи линейного целочисленного программирования.

 Целевая функция имеет вид:

                                                                                                        (11)

 

где  - коэффициенты, соответствующие заданным размерам раскроя,  - искомая целочисленная переменная, соответствующая количеству раскроев, заданное - ой длины.

Обычно для раскроя используется исходный материал сложной формы, поэтому для каждого раскроя единицы материала должно выполняться следующее ограничение:

                                                                                                             (12)

 

где  - коэффициенты, соответствующе длинам раскраиваемого материала.

При динамическом раскрое на каждый момент времени существует потребность в исходном материале, которую можно описать с помощью ограничений

 

 

                                                                                       (13)

где -элементы матрицы коэффициентов,  - число допущенных к рассмотрению раскроев,  - количество ограничений.

 Из анализа методов решения проблемы оптимизации раскроя, очевидно, что существует множество методов решения задачи (1) при ограничениях (2),(3), среди которых наиболее известные:

-                   метод динамического программирования;

-                   метод Гомори;

-                   метод Балаша;

-                   метод ветвей и границ.

Однако, они оказываются не эффективными для решения реальных производственных задач.

Метод замещений свободен от вышеназванных недостатков, поэтому для решения поставленной задачи целесообразно применение метода замещений [7].

Метод замещений - это точный метод решения задач на графах, использующий поиск в глубину с возвращением. В основе метода лежит фундаментальный принцип парных замещений.

Под парой замещения, в зависимости от характера задачи, понимается либо пара ребер, либо пара вершин, т.е. два каких-либо однородных элемента графа.

Один элемент является удаляемым, а другой – добавляемым.

Элементарная операция замещения заключается в замене первого элемента вторым.

В результате выполнения элементарной операции замещения в исследуемом подграфе происходит изменение таких параметров как вес подграфа, структура подграфа, степени вершин подграфа, число компонент его связности и др.

Это обстоятельство является важнейшим с точки зрения вычислительного эффекта.

Алгоритмы, построенные на базе метода замещений, имеют процедуры, отслеживающие текущее состояние упомянутых параметров. Это дает возможность:

-                   более точно выбирать дальнейшее направление вычислительного процесса;

-                   использовать новые виды математических ограничений (векторы топологии);

-                   сокращать объемы вычислительных затрат при использовании вычислительной техники.

В основе построения дерева замещений лежит следующая вычислительная схема, составляющая метод замещений.

1. Вычисляется значение верхней границы в соответствии с (9) и уточняется по правилу (10).

2. Ветвление происходит по следующей многошаговой схеме.

Если в корневом узле ДЗ , то генерируется некоторое множество пар замещений с одновременной проверкой каждой пары на превышение верхней границы по (9) и необратимое нарушение топологии искомого подграфа по (10).

В необходимом случае пара замещения не включается в список узлов ДЗ, подлежащих упорядочению. Допущенные к рассмотрению узлы упорядочиваются по возрастанию разности .

Аналогично выше изложенному выполняется ветвление и на других ярусах ДЗ. Продвижение вглубь ДЗ выполняется до тех пор, пока не будет получен нуль-узел или не будет достигнут номер максимального яруса ДЗ.

В первом случае уточняется верхняя граница  и номер максимального яруса ДЗ, а списки замещенных и заместивших ребер переписываются из ДЗР в СЗР.

Все узлы ДЗ, находящиеся справа от нуль - узла на данном ярусе, не исследуются, а отсекаются.

Отсечение узлов-братьев, находящихся справа от исследуемого узла, выполняется и в том случае, если достигнута верхняя граница без появления нуль - узла.

В обоих случаях происходит возвращение на следующий более высокий ярус ДЗ и т.д.

3. Отсечение бесперспективных ветвлений ДЗ по номеру максимального яруса, полученному в ближайшем предшествующем нуль -узле, выполняется путем прекращения генерации узлов-сыновей.

4. Если при генерации пары замещения появляется подграф с увеличивающейся степенью вершины, то данная пара замещения исключается из списка сгенерированных пар.

Количество узлов, генерируемых на каждом ярусе ДЗ, с одной стороны, должно быть минимальным, чтобы уменьшить трудоемкость решения, а с другой, - достаточным, чтобы гарантировать точное решение.

Количество пар замещений (узлов-братьев) ограничено декартовым произведением

                                                                                                             (14)

где  - множество ребер  подграфа  инцидентных вершине со степенью большей или равной степени одной из вершин той же доли искомого подграфа,  - множество ребер  подграфа , со степенью меньшей или равной степени одной из вершин той же доли искомого подграфа.

При этом множества ребер  и  не должны иметь общей вершины, степень которой проверяется.

В каждом узле ДЗ генерация множества  пар замещений – сынов данного узла на -м ярусе ДЗ приводит к единственному и точному решению задач (1) в одном из его висячих узлов на ярусе .

Проверка степеней вершин промежуточных подграфов выполняется в порядке возрастания номеров вершин сначала в первой доле двудольного графа, затем - во второй доле графа.

Алгоритм решения оптимизационной задачи с помощью метода замещений рассмотрим на примере задачи максимизации.

Шаг 1. Множество ребер  двудольного графа  упорядочивается по возрастанию их весов .

Шаг 2. Множество ребер  двудольного графа  разделяется на два подмножества: первое подмножество  содержащее ребра максимального веса и второе подмножество  содержащее ребра минимального веса.

Шаг 3. Построение дерева решений или точнее дерева замещений (ДЗ) начинается с корневого узла. Если топология начального подграфа  удовлетворяет заданным ограничениям из набора (2.3.2-2.3.6), то решение задачи получено.

Шаг 4. В противном случае строится ДЗ, в каждом узле которого конструируется некий промежуточный подграф  по вышеизложенной схеме построения ДЗ.

При этом узлы-братья, находящиеся на одном ярусе ДЗ, упорядочиваются по возрастанию разности весов пары замещений.

Это позволяет отсекать узлы-братья, находящиеся справа, в том случае, если новый узел-брат достиг требуемой топологии.

Шаг 5. Отсечение бесперспективных ветвей ДЗ выполняется по следующим критериям:

а) по превышению верхней границы,

б) по необратимому нарушению топологии подграфа ,

в) по прогнозному значению веса промежуточного подграфа,

г) под достижению запрещенных значений тех величин, которые заданы дополнительными ограничениями по условию задачи.

Шаг 6. Возврат на верхний ярус ДЗ выполняется по критерию (а).

Переход к узлу-брату, находящемуся справа, выполняется по критериям (б), (в), (г).

Описанный выше метод замещений удобен для решения задачи раскроя, а именно в той ее постановке, которая относится к генерированию раскроя мерного материала с требованием целочисленности переменных.

В этом случае требуется получить максимально экономичный раскрой для каждого профиля на текущий момент времени, то есть при известной матрице ограничений.

Поэтому целевая функция будет иметь вид (11), конечность длины раскраиваемого материала моделируется ограничением (12), а потребность в исходном материале - ограничениями (13).

Ограничения (13) определяются состоянием буферного склада: при дефиците исходного материала с размером  диапазон значений переменной  сдвигается в сторону увеличения, а при избытке - в сторону уменьшения.

Пусть множество вершин первой доли двудольного графа  соответствует заданному множеству размеров заготовок , где   - множество вершин второй доли двудольного графа  соответствует доступным способам раскроя профиля на некоторые из заготовок  (рис. 1).

 

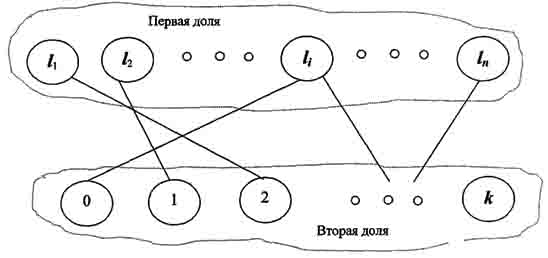
Рис. 1. Моделирование задачи раскроя на двудольном графе.

 

Ребра, соединяющие вершины первой и второй доли графа соответствуют матрице ограничений, моделирующей требования к комплектности заготовок.

Для решения задачи требуется найти однозначное соответствие между вершинами первой и второй доли графа.

Для выполнения этого требования введем вектор закрепленных степеней для первой доли графа

  

где  - степень вершины с номером .

Очевидно, что для задачи раскроя

Векторы допустимых степеней для второй доли графа

 и

формируются, исходя из имеющейся матрицы ограничений для каждой новой задачи генерирования раскроя.

Вектор подвижных степеней  для первой доли графа определяет максимальные степени вершин графа.

Векторы топологии оказывают существенное влияние на вычислительный процесс.

В частности, при нахождении некоторого решения на каждом шаге осуществляется прежде всего проверка допустимости топологии полученного промежуточного подграфа.

Несоответствие топологии подграфа хотя бы одному из указанных условий ведет к непринятию полученного решения как оптимального.

Таким образом, векторы топологии позволяют сузить область допустимых решений, что ведет к значительному уменьшению трудоемкости решения задачи.

С учетом вышесказанного вычислительная схема решения целочисленной задачи раскроя может быть сформирована следующим образом:

1. На основе ограничений (12 - 13) формируются векторы топологии:

• вектор закрепленных степеней  для первой доли графа, которая моделирует допустимые длины раскроя;

• векторы допустимых степеней

  

для второй доли графа, моделирующей доступные способы раскроя профиля на некоторые из нужных заготовок.

2. Формируется список ребер Е двудольного графа G(V₁,V₂,E), взвешенных по произведениям и упорядоченных по убыванию их весов.

Множеств ребер  разделяется на два подмножества: первое подмножество , содержащее ребра максимального веса и второе подмножество , содержащее ребра минимального веса.

3. Формируется дерево замещений (ДЗ) путем построения допустимых кортежей пар замещений с учетом условий (12 - 13) и векторов топологии.

Конструирование подграфа в каждом узле дерева выполняется путем замещения одного из ребер первого подмножества на одно из ребер второго подмножества, т.е. ребра  являются кандидатами на удаление, а ребра  - кандидаты на добавление в ДЗ.

При этом ребро, замещенное в узле-предке, не может стать замещающим в узлах-потомках, а заместившее ребро в узле-предке не должно замещаться в узлах-потомках.

4. Среди допустимых кортежей пар замещений отыскивается эффективный кортеж, доставляющий оптимум искомому подграфу  по (11) и (12 - 13).

Таким образом, выбранный и обоснованный метод решения задачи оптимизации раскроя материала позволяет повысить эффективность раскройно-заготовительного производства на основе сформулированного принципа парных реберных замещений для двудольных графов, принципа парных замещений, сформирована вычислительная схема решения целочисленной задачи раскроя.

Показано, что реальные условия производственного характера можно формализовать векторами топологии: вектором закрепленных степеней и вектором подвижных степеней и использовать их в качестве ограничений для первой доли двудольного графа, моделирующей допустимые длины раскроя, векторы допустимых степеней – для второй доли двудольного графа, моделирующей доступные способы раскроя исходного материала.

 

Литература

 

1.                  Автоматизированное производство и проектирование в машиностроении. / Под ред. Ю.М. Соломенцева, В.Г. Митрофанова. - М.: Машиностроение, 1986. - 256 с.

2.                  Аверьянова Н.К., Бухвалов A.B. Опыт внедрения программы линейного раскроя в судостроении // Математическое обеспечение рационального раскроя в системах автоматизированного проектирования: Тез. докл. всесоюз. конф., Уфа, 1987, с. 2 - 3.

3.                  Алгоритмы и программы решения задач на графах и сетях. - Новосибирск: Наука, Сиб.отд., 1990. - 513 с.

4.                  Бабаев В.Ф. Оптимальный раскрой материалов с помощью ЭВМ. - М.: Машиностроение, 1982. - 167 с.

5.                  Беллман         Р. Динамическое программирование. - М.: ИЛ., 1960. - 400 с.

6.                  Габитов          В.А., Мухачева A.C., Федорова H.H. Предоптимаизационный выбор алгоритма решения задачи линейного целочисленного раскроя // В кн.: Принятие решений в условиях неопределенности, Уфа, 1996, с. 17-22.

7.                  Горшков А.Ф., Соломенцев Ю.М. Отыскание экстремальных каркасов с предписанными степенями вершин методом замещений. //ДАН, 1996. Т.347, № 4, с.443-445.

8.                  Горшков А.Ф., Соломенцев Ю.М. Применимость реберных замещений в классе комбинаторных задач на графах. //ДАН, 1994. Т.337, № 2, с.151-153.

9.                  Канторович Л.В., Залгаллер В.А. Рациональный раскрой промышленных материалов. - Новосибирск: Наука, Сибирское отделение, 1971 - 320 с.

 

Поступила в редакцию 03.03.2017 г.