Теория поступательного движения инерцоида с ускоряемыми грузами
Берников Василий Русланович,
начальник лаборатории ЗАО «НПП «Салют-27».
На основании обычных классических представлений физической механики рассмотрим возможность поступательного движения инерцоида с периодически ускоряемыми и замедляемыми грузами. Внутренние силы в ряде случаев являются причиной появления внешних сил, приложенных к системе [1, с.197-202], [2, с.139-142], [3, с.364]. Возможность перемещения замкнутых систем за счёт внутренних сил доказана в [4, с.28-41], [5, с.142-146], [6, с.105-107], [7, с.230-233].
Рассмотрим тело массой М, которое нужно привести в состояние поступательного движения с помощью двух синхронно и симметрично вращающихся в противоположных направлениях грузов массой m (рис.1).
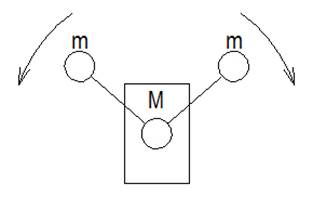
Рис. 1.
Пусть грузы движутся с постоянным ускорением в первой части полуокружности и с замедлением во второй части полуокружности, причём для расчёта сил ускоряемых грузов на тело пусть его масса будет много больше массы грузов, тогда можно пренебречь влиянием движения тела на грузы. Запишем формулу продольной скорости (поперечную скорость грузов не учитываем, так как они компенсируются) груза в первой полуокружности в скалярной форме (рис.2)
vII = vsinΨ, (1)
где v – скорость груза по касательной к окружности, Ψ – угол между радиусом R и прямой, разделяющей пополам окружность.
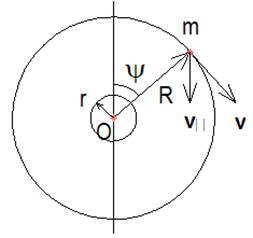
Рис. 2.
Скорость груза по касательной к окружности будет
v = eоt. (2)
Угловая скорость груза
dΨ/dt = v /R (3)
или согласно формуле (2)
dΨ/dt = eоt /R. (4)
Интегрируя выражение (4) получим
Ψ = eоt2/2R. (5)
Подставим (2) и (5) в (1), тогда
vII = eоt sin (eоt2/2R). (6)
Производная по времени продольной скорости в формуле (6) – это ускорение
ɑ = eо[sin (eоt2/2R) + (eоt2/R)cos(eоt2/2R)]. (7)
Или, используя (5)
ɑ = eо(sin Ψ + 2Ψcos Ψ). (8)
График ускорения ɑ в зависимости от угла Ψ представлен на рисунке 3.
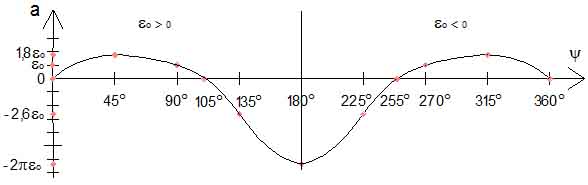
Рис. 3.
По второму закону Ньютона продольная сила, действующая на груз будет
Fг = mɑ. (9)
По третьему закону Ньютона ей будет противодействовать продольная сила от тела М, которая, очевидно, зависит от соотношения радиуса r его вала, радиуса R от центра вала до центра груза и угла Ψ (рис.2)
Fт1 = -(R/r)mɑ sin Ψ (10)
или
Fт1 = -(R/r)meо (sin2 Ψ + 2Ψcos Ψ sin Ψ). (11)
Знак «минус» в формулах (10) и (11) указывает на противоположное направление силы
Вычислим среднее значение в первой полуокружности
p
Fт1 ср = - (R/pr)meо ∫ (sin2 Ψ + 2Ψcos Ψ sin Ψ)d Ψ = 0. (12)
0
Очевидно, и во второй полуокружности с замедлением средняя сила, действующая на тело, также будет равна нулю. То есть в этом случае поступательного движения не будет.
Рассмотрим график на рисунке 3: необходимо уменьшить по абсолютной величине отрицательную часть ускорения в интервале от 105° до 180° в первой полуокружности и от 180° до 255° во второй полуокружности. Для этого в этих интервалах груз пусть движется равномерно по окружности, тогда отрицательная часть уменьшится по абсолютной величине. Запишем формулу продольной скорости груза в первой полуокружности в интервале от 105° до 180°
vII = vо sinΨ, (13)
где vо – постоянная скорость груза по касательной к окружности.
Угловая скорость груза
dΨ/dt = vо /R. (14)
Интегрируя выражение (14) получим
Ψ = vоt/R. (15)
Подставим (15) в (13)
vII = vо sin (vоt/R). (16)
Производная по времени продольной скорости в формуле (16) – это ускорение
ɑ = (vо2/R)cos(vоt/R) (17)
Найдём скорость vо в точке 105°(1,836 рад), используя формулу (2)
vо = eоt. (18)
Время t находим иэ формулы (5)
t =Ö(2RΨ/eо). (19)
Подставим (19) в (18) получим
vо =Ö(2ReоΨ). (20)
Так как Ψ = 1,836 рад, тогда
vо =Ö(2Reо1,836) » Ö(3,7Reо). (21)
Подставим (21) в (17) получим ускорение в интервале от 105° до 180°
ɑ = 3,7eоcos(vоt/R) = 3,7eоcosΨ. (22)
График ускорения в интервале от 0° до 105° по формуле (8) и от 105° до 180° по формуле (22) представлен на рисунке 4, где видно уменьшенную величину отрицательного ускорения.
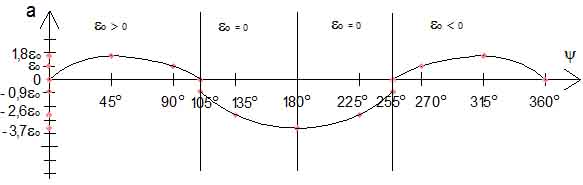
Рис. 4.
Аналогично формуле (10) сила, действующая на тело
Fт2 = -(vо2/r)mcosΨsinΨ. (23)
Подставим (21) в (23) получим силу, действующую на тело в интервале от 105° до 180° при движении по окружности с постоянной скоростью vо
Fт2 = -3,7(R/r)meо cosΨsinΨ. (23)
Вычислим среднее значение
p
Fт2 ср = - 3,7 (R/((p-1,836)r)meо ∫(cos Ψ sin Ψ)d Ψ » (R/r)meо. (24)
1,836
Теперь вычислим среднее значение в интервале от 0° до 105°(1,836 рад) груза, движущегося с ускорением согласно формуле (11)
1,836
Fт1 ср = - (R/1,836r)meо ∫(sin2 Ψ + 2Ψcos Ψ sin Ψ)d Ψ » -1,4(R/r)meо. (25)
0
Сложим средние значения Fт1 ср и Fт2 ср получим среднее значение в интервале от 0° до 180°
Fт ср = Fт1 ср + Fт2 ср = -0,4(R/r)meо. (26)
Таким образом, в этом случае тело будет совершать поступательное движение под действием силы определяемой формулой (26).
Пусть R=0,1м; r=0,0025м; m=0,1кг; eо =5 м/с2, тогда абсолютная величина силы будет
|Fт ср| = 0,4× (0,1/0,0025) × 0,1× 5 = 8 Н.
Литература
1 Шипов Г.И. Теория физического вакуума. Теория эксперименты и технологии. 2-е изд., – М.:Наука,1996, 456с.
2 Геронимус Я. Л. Теоретическая механика (очерки об основных положениях): Главная редакция физико-математической литературы изд-ва «Наука», 1973г., 512с.).
3 Курс теоретической механики: учебник / А.А.Яблонский, В.М.Никифорова. – 15-е изд., стер. – М.: КНОРУС, 2010, 608с.
4 Турышев М.В., О движении замкнутых систем, или при каких условиях не выполняется закон сохранения импульса, «Естественные и технические науки», №3(29), 2007, ISSN 1684-2626.
5 Берников В.Р., Возможность перемещения замкнутой системы за счёт внутренних сил в классической механике, «Актуальные проблемы современной науки», №6(91), 2016 г., ISSN 1680-2721.
6 Берников В.Р., Перемещение замкнутой системы тел за счёт внутренних сил в классической механике, «Актуальные проблемы современной науки», №2(93), 2017 г., ISSN 1680-2721.
7 Берников В.Р., Классический способ перемещения замкнутых систем за счёт внутренних сил, «Актуальные проблемы современной науки», №4(95), 2017 г., ISSN 1680-2721.
Поступила в редакцию 13.11.2017 г.