Теория неустойчивости. Спектральные методы и критерии хаоса

 

Перевозников Евгений Николаевич,

кандидат физико-математических наук, доцент, старший научный сотрудник Военно-космической академии им. А. Ф. Можайского,

Скворцов Генрих Евгеньевич,

кандидат физико-математических наук, старший научный сотрудник Санкт-Петербургского государственного университета.

 

Развивается теория неустойчивости, предлагаемая авторами. Дается ее раздел, в котором получается система аналитических критериев хаоса. Для этого используются два варианта метода линейного спектра и вводится новый метод нелинейного спектра. Приводится пример, демонстрирующий методы и критерии.

Ключевые слова: неустойчивости, спектральные критерии хаоса.

 

Theory instability, proposed by the authors, is developed. The system of analytical criteria for chaos is optained. For this purpose, two variants of the method of linear spectrum, and a new method of non-linear spectrum is used. The example showing the methods and criteria is given.

Keywords: instability, spectral criteria of chaos.

 

1. В работах [1-5] были даны основы теории неустойчивости (ТНУ): определения неустойчивости, ряд законов и методов.

Последние занимают основное место в теории и требуют своего развития и специализации для разных задач. Отметим, что развиваемая теория не сводится к теории устойчивости Ляпунова, она шире, включает в себя теорию катастроф, синергетику, различные качественные переходы. Отметим, что, начиная с работы [6], авторами обнаружен целый ряд неустойчивостей в ударных волнах, в плазменных потоках реактивных двигателей, в динамике заряженных систем в сильных электрических полях, в деформационных процессах в полимерах.

Полученные при этом результаты и опыт позволили начать формулировать теорию неустойчивости, включая и хаотические режимы. При этом основным направлением является получение аналитических критериев. Регулярный подход в этом направлении до статей [1-5] отсутствовал.

В данной работе результаты, полученные в [1-5], дополнены и систематизированы в виде набора спектральных методов и критериев хаоса для трехмерных динамических систем. Ограничение трехмерными системами позволяет отразить основные стороны проблемы в достаточно простом виде.

Исходной является система уравнений

                                 (1)

с начальными условиями . Правые части уравнений (1) — действия, нелинейные функции второго порядка по нелинейности. Этого достаточно для получения представительных результатов.

2. Стандартный спектральный метод заключается в линеаризации системы (1) относительно стационарных решений – нулей действий, получение спектрального уравнения и его анализа. В процессе анализа получаются комплексы из коэффициентов спектрального уравнения, определяющих наличие хаотического режима – критериев хаоса.

Полезным расширением стандартного метода является метод локального спектра, состоящий в линеаризации относительно произвольного исходного состояния. В этом случае критерии будут зависеть и от начальных условий. Заметим, что неустойчивость и хаос в общем случае зависят от выбора начальных условий.

В общем случае в исходной нелинейной системе (1) может быть шесть стационарных решений и необходимо просматривать их на наличие неустойчивости и хаоса и выбирать соответствующие начальные условия в локальном варианте.

Линеаризация системы (1) в произвольной точке приводит к следующему спектральному уравнению (СУ)

 ,                                                                                            (2)

где λ — спектральный параметр, s, p, q — спектральные коэффициенты, зависящие от частных производных действий  взятых в точке . Используя критерии неустойчивости и хаоса, полученные на основе СУ (2), в которые входят начальные значения, определяем последние из условия наличия хаоса.

Обобщением стандартного метода линейного спектра является метод нелинейного спектра (НЛС), состоящий в следующем: символ временных производных в (1) заменяется на параметр λ (который можно считать нелинейным собственным значением). Полученная система алгебраических уравнений разрешается относительно динамических переменных , из них выбирается наиболее полная зависимость, содержащая сингулярность. Найденная сингулярная зависимость подобна спектральному уравнению и позволяет получить критерии неустойчивости и хаоса.

Ниже этот метод демонстрируется на примере.

3. Результаты, предсказываемые полученными критериями, согласуются с наблюдаемыми эффектами и численными решениями различных задач. Критерии отражают характерные признаки хаоса: колебательность и взаимодействие растущей и затухающей мод, что соответствует наличию в спектре седлообразного фокуса.

Основные критерии, отражающие указанные признаки имеют вид

 .                                                              (3)

Первое неравенство (3) есть условие неустойчивости, второе — отражает наличие колебаний, третье — седлообразный характер спектра.

Критерии (3) становятся очевидными, если учесть их связь и коэффициентов СУ с собственными значениями, для СУ (3) равными

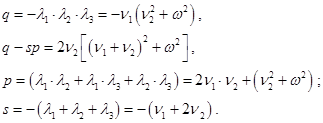                                                 (4)

 

 

где  вещественный и комплексно-сопряженные корни СУ (3).

Следующим критерием хаоса является выражение       

 .                                                                                                   (5)

Это следствие условия бифуркации корней и вытекает из решения приведенного СУ.

 

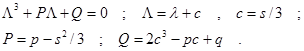                                                     (6)

 

Очевидно, что картина спектра такова: если Q > 0 , то в левой спектральной полуплоскости вещественное собственное значение, в правой два сопряженных; если Q < 0 , то наоборот. Такая картина соответствует условиям хаоса.

 Коэффициент s имеет и самостоятельное значение в виду связи с

.                                                                                          (7)

 

Величина определяет изменение фазового объема системы динамических уравнений.

При  < 0 — фазовый объем убывает — система диссипативная; при  = 0 — система нейтральная; при  > 0 — фазовый объем увеличивается — система активная. Хаос возможен во всех вариантах поведения системы и называется соответственно.

При p ≤ 0 приведённые критерии части наличия колебательности необходимо заменить общим критерием

D = (q – q₁)(q – q₂) > 0 , q < q₁ или q > q₂,                                                             (8)

при P < 0,

 

или q — любое, если P > 0.

4. В качестве примера демонстрации критериев выберем одну из моделей хаотической динамики — модель Спротта /7/

.                                (9)

Показатель типа динамики  В зависимости от выбора начального условия —  можно получить все три вида хаоса.

По методу нелинейного спектра (как наиболее простого) из системы (9) имеем

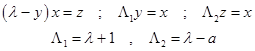.                                                                 (10)

 

Разрешая систему (10) относительно динамических переменных  и, выбирая наиболее представительную из них в данном случае х, получаем

.                                                                           (11)

Сингулярная зависимость соответствует , откуда получаем спектральное уравнение по методу НЛС

.                                                                             (12)

Критерии К1,2,3 удовлетворяются при , при этом К3 > 0. Таким образом все критерии указывают на наличие хаоса. Решение спектрального уравнения (12) дает

.                                                                   (13)

Это также удовлетворяет условиям хаоса при , причем при  хаос активный.

Для сравнения методов нелинейного и линейного спектров рассмотрим нелокальное спектральное уравнение, коэффициенты которого равны

                (14)

Для упрощения анализа примем . С учетом этого, из условий границы

хаоса (К1 = 0 , p > 0) получаем оценку граничного значения

,                                                                  (15)

 

с которого начинается хаотический режим.

Отметим, что различие результатов двух методов естественно, так как в методе локального спектра получили граничные начальные условия, а в методе нелинейного спектра исходили из нулевых . Полное согласие результатов методов достигается при стандартном подходе для нулевого стационарного состояния.

В заключении отметим, что главные результат работы состоят в формулировке простых эффективных методов и критериев хаоса. Их наглядность и простота позволяет конструктивно выявлять хаотическое поведение в трехмерных задачах с любым видом действий, а также обобщать на системы большей размерности. Очевидно, что в отношении самого феномена хаоса имеется достаточно проблем, которые еще предстоит решить. Например вопросы о времени развития хаоса, о чередовании режимов — перемежаемости, об амплитуде хаотических колебаний, о частотном спектре и т.д. Но это вопросы следующих исследований.

 

Литература

 

1.                  Перевозников Е.Н., Скворцов Г.Е., Физическая неустойчивость и качественные переходы, Materialy X miedzynarodwej naukowi-praktycznej konferencji, v 30, 2014, p (79-84).

2.                  Скворцов Г.Е., Перевозников Е.Н., Динамические качественные переходы, Materialy X miedzynarodwej naukowi-praktycznej konferencji, Eвропейская наука ХХ1 века (Польша, Przemysl май 2014), v 31, 2014, p (82-84).

3.                  Скворцов Г.Е, Перевозников Е.Н., Основы общей теории неустойчивости, Журнал научных публикаций аспирантов и докторантов, 2015 № 7, (85-87)с.

4.                  Скворцов Г.Е., Перевозников Е.Н., Сингулярно-динамические критерии неустойчивости и хаоса, Международный научно-исследовательский журнал, физико-математические науки, 2015, №9, ч. 3, (91-93).

5.                  Скворцов Г.Е.,О закономерностях неравновесных процессов, Письма ЖТФ, т.16 вып. 17, 1990, с. (15-17).

6.                  Перевозников Е.Н., Скворцов Г.Е., К теории устойчивости неравновесных систем, ЖТФ, вып.12, № 52, 1982, с (2353-2361).

7.                  Кузнецов С.П., Динамический хаос, М., 2006, 356 с.

 

Поступила в редакцию 26.12.2016 г.